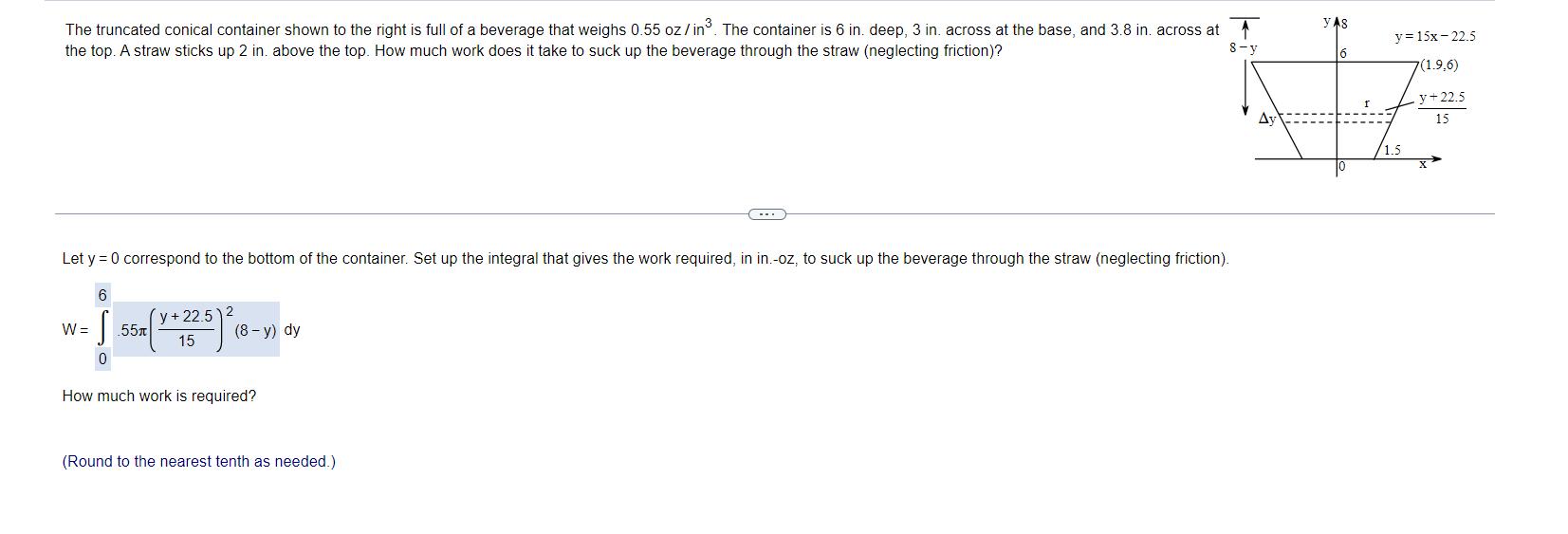
The truncated conical container shown to the right is full of a beverage that weighs 0.55 oz/in. The container is 6 in. deep, 3 in. across at the base, and 3.8 in. across at the top. A straw sticks up 2 in. above the top. How much work does it take to suck up the beverage through the straw (neglecting friction)? 8-y Let y = 0 correspond to the bottom of the container. Set up the integral that gives the work required, in in.-oz, to suck up the beverage through the straw (neglecting friction). 6 S 0 W = 55 y + 22.5 15 2 (8-y) dy How much work is required? (Round to the nearest tenth as needed.) Ay YAS 6 y = 15x-22.5 (1.9,6) 1.5 .y+22.5 15