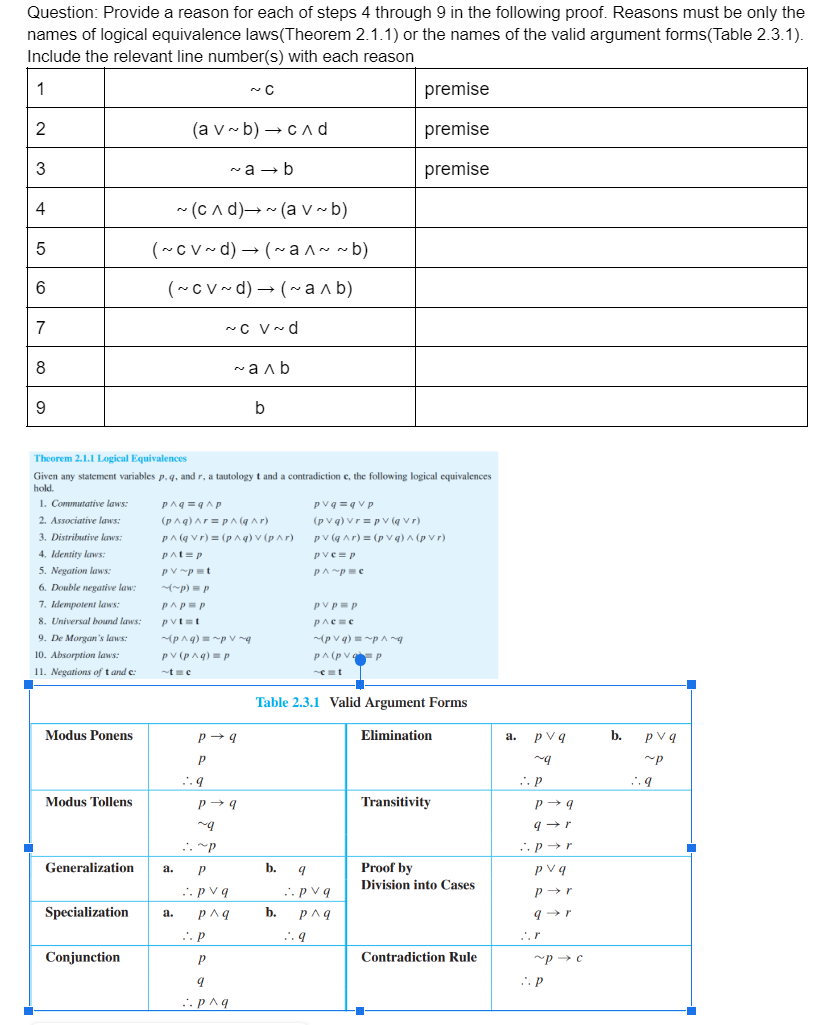
Theorem $2\mathrm{.}1\mathrm{.}1$ Logical Equivalences

Given any statement variables $p,q,$ and $r,$ a tautology $t$ and a contradiction $c,$ the following logical equivalences

hold.

Commutative laws:

Assaciative lavs:

Distributive laws:

Identity laws:

Negation laws:

Double negative law;

Idempoient laws:

Universal bound laws:

De Morgan's laws:

Absorption laws:

Negations of $t$ and $c$ :

$p^{{?}^{?}}q=q^{{?}^{?}}p$

$(p^{{?}^{?}}q{)}^{{?}^{?}}r=p^{{?}^{?}}(q^{{?}^{?}}r)$

$p^{{?}^{?}}(qvvr)=(p^{{?}^{?}}q)vv(p^{{?}^{?}}r)$

$p^{{?}^{?}}t=p$

$pvvp-=t$

$(p)=p$

$p^{{?}^{?}}p=p$

$pvvt=t$

$(p^{{?}^{?}}q)=pvvq$

$pvv(p^{{?}^{?}}q)=p$

$t-=c$

$pvvq=qvvp$

$(pvvq)vvr=pvv(qvvr)$

$pvv(q^{{?}^{?}}r)=(pvvq{)}^{{?}^{?}}(pvvr)$

$pvvc=p$

$p^{{?}^{?}}p-=c$

$pvvp=p$

$p^{{?}^{?}}c=c$

$(pvvq)=p^{{?}^{?}}q$

$=t$