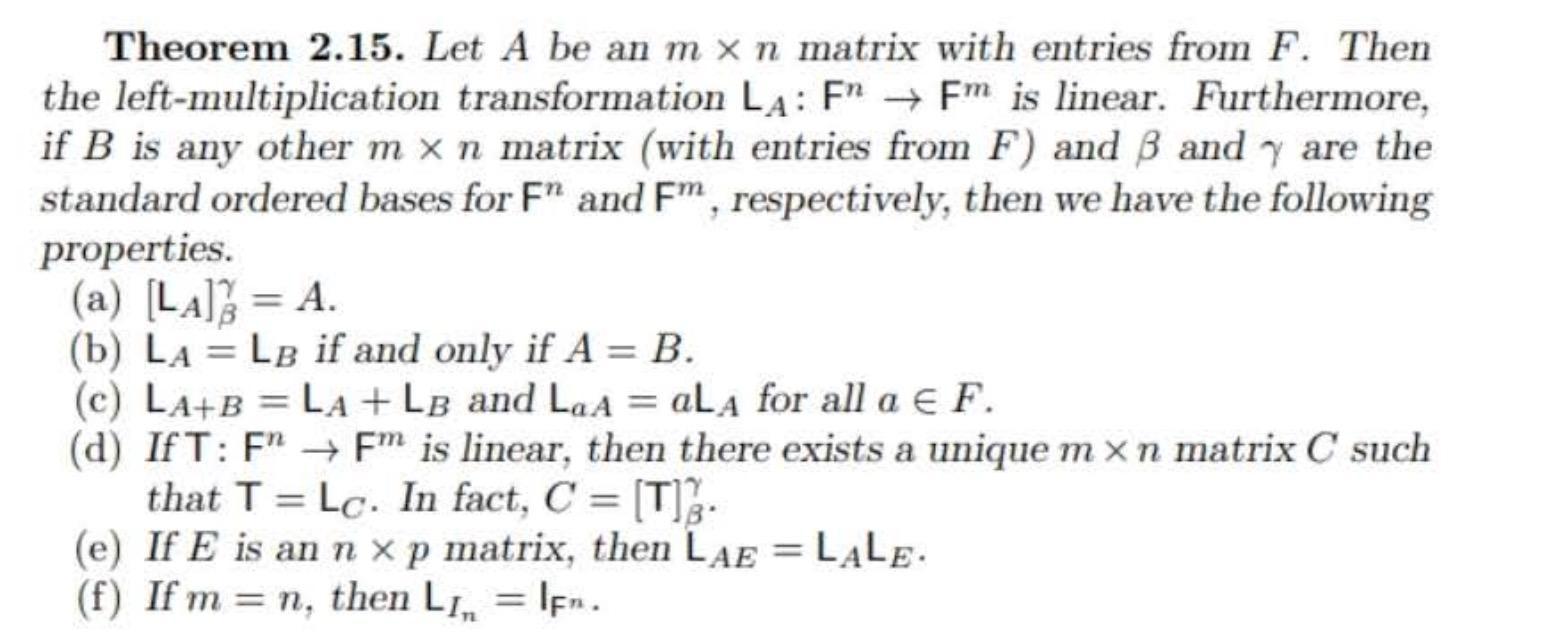
Theorem 2.15. Let A be an m x n matrix with entries from F. Then the left-multiplication transformation LA: F Fm is linear. Furthermore, if B is any other m x n matrix (with entries from F) and 3 andy are the standard ordered bases for F" and Fm, respectively, then we have the following properties. (a) [LA] = A. (b) LA = LB if and only if A= B. (c) LA+B=LA + LB and LaA = aLA for all a F. (d) IfT: F Fm is linear, then there exists a unique m x n matrix C such that T = Lc. In fact, C = [T]. (e) If E is an n xp matrix, then LAELALE. (f) If m= n, then L= IF.