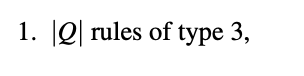
???

If A is a pushdown automaton, then L(A) is a context-free language. Proof. Non-constructive proof of existence. Let B be a PDA equivalent to A constructed with the specifications given in Lemma 3.2. Thus, in particular, L(B) = L(A). Now, the computation of each w = a an E L(B) produces at least one accepting computation path. Select one such path and plot the pairs (qi, Y), qi E Q, in the order that they appear in the path. Now, since each variable used in the construction of the rules is indexed with a pair in QxQ, there are at most, 1. Q rules of type 3, 2. Q rules of type 2, and 3. Q42 rules of type 1. Thus, the total number of rules that can be generated by randomly selecting inputs w * to PDA B is bounded above by C = |Q|(1+|0|+101121). Consequently, by running he method Algorithm 4 Generation of CFG G 1: procedure RULE GENERATOR(On input: ; w E*, B a PDA) 2: Run B on w. 3: if B rejects then 4: 5: 6: 7: 8: 9: end if 10: end procedure return: no rules produced. else Select an accepting computing branch Plot the pairs (qi, \y\) return: list of rules. (3.14) on a large enough number of different w E E*, the set of all rules of a CFG for producing L(B) = L(A) will be obtained. Corollary 3.2. Each context-free language is generated with a CFG whose rules are of the form V E, V aUb, a, b literals, and V UZ. Proof. Is a direct consequence of the proof of Theorem 3.7.