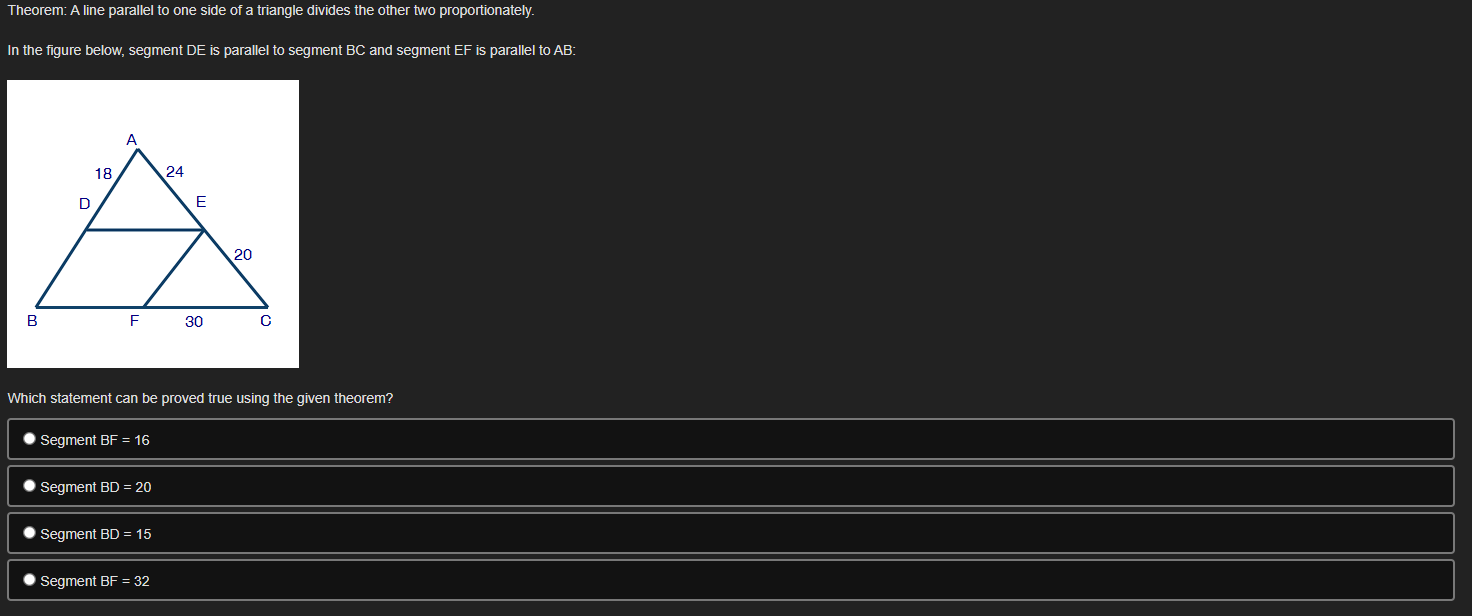
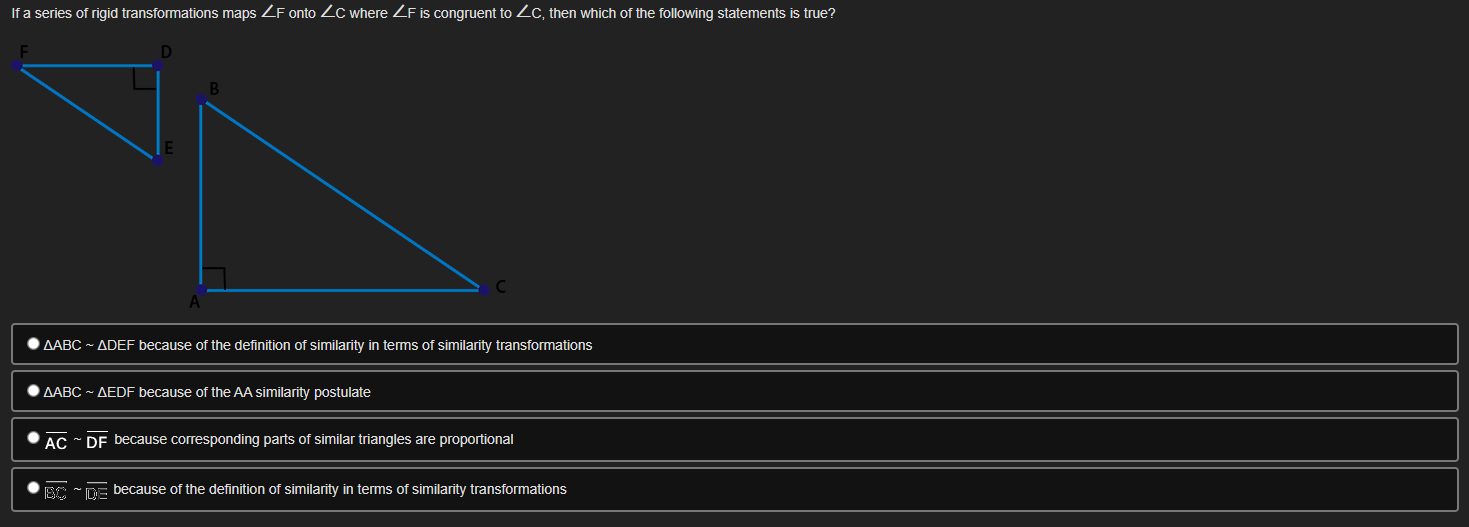
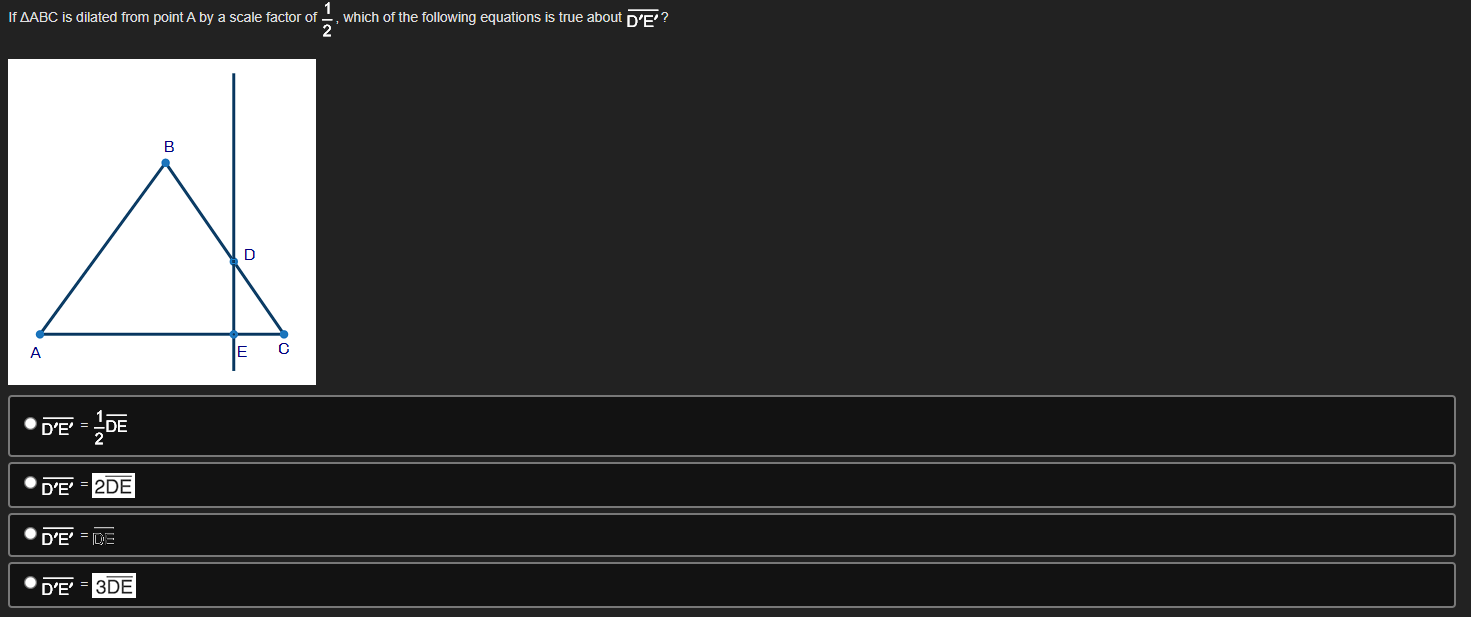
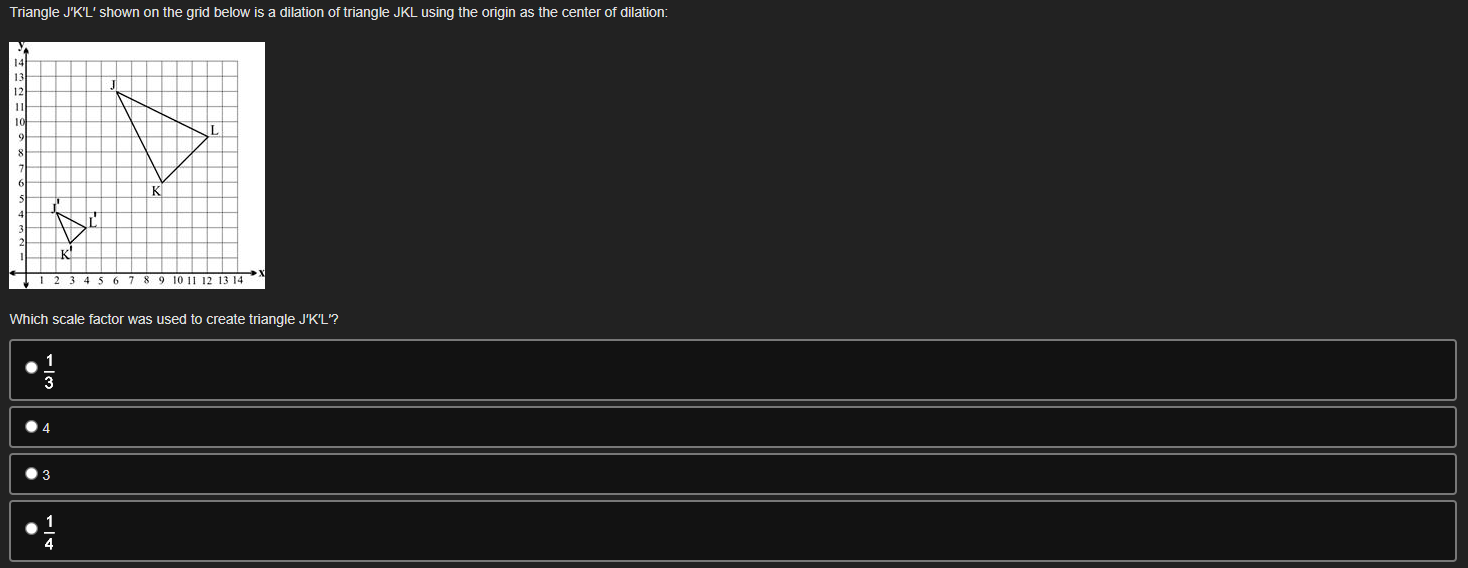
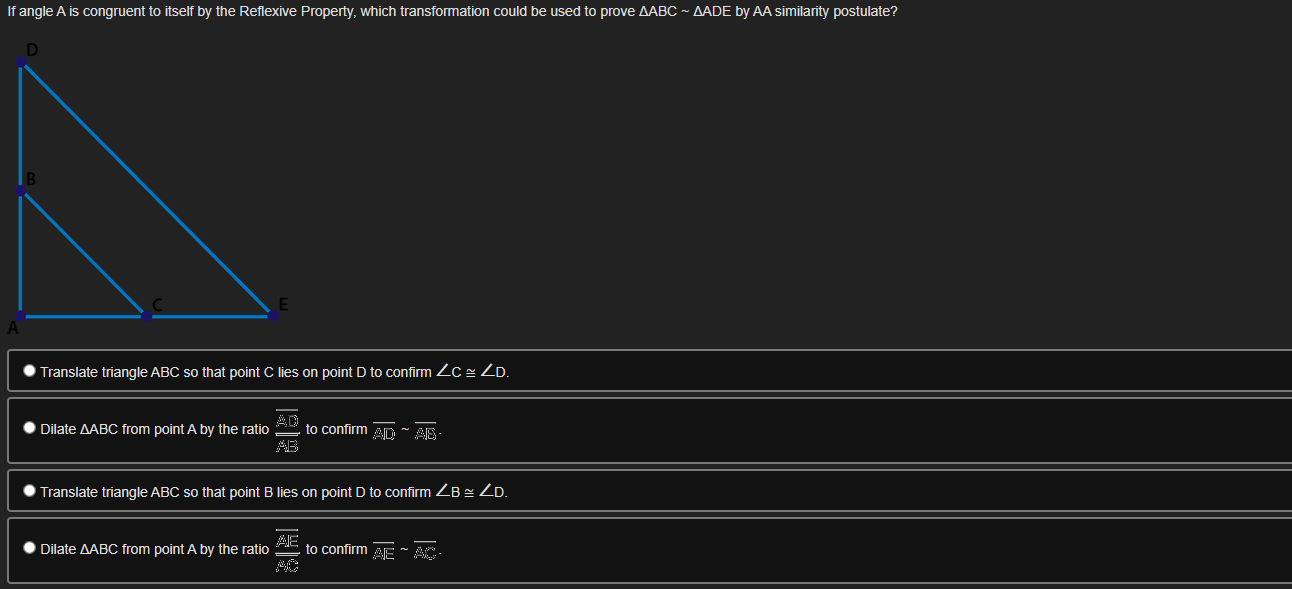
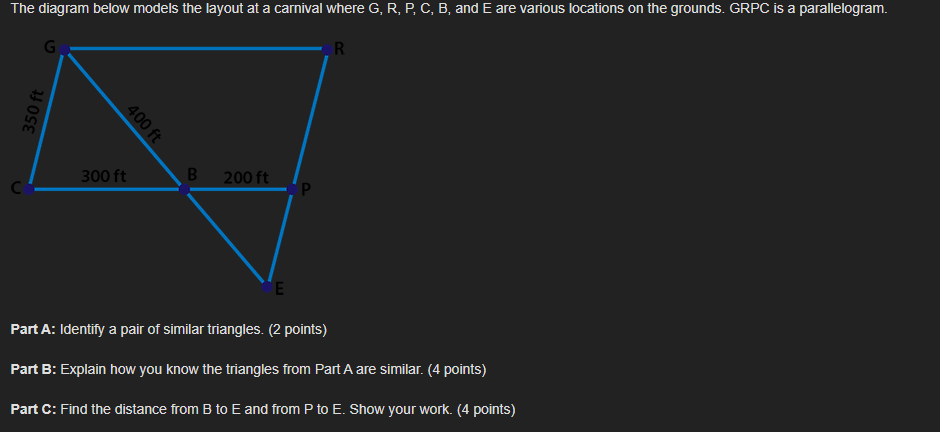
Theorem: A line parallel to one side of a triangle divides the other two proportionately. In the figure below, segment DE is parallel to segment BC and segment EF is parallel to AB: 18 24 D 20 B F 30 C Which statement can be proved true using the given theorem? Segment BF = 16 Segment BD = 20 Segment BD = 15 Segment BF = 32If a series of rigid transformations maps ZF onto LC where ZF is congruent to LC, then which of the following statements is true? F D B C . AABC ~ ADEF because of the definition of similarity in terms of similarity transformations . AABC ~ AEDF because of the AA similarity postulate AC ~ DF because corresponding parts of similar triangles are proportional BC because of the definition of similarity in terms of similarity transformationsIf AABC is dilated from point A by a scale factor of % . which of the following equations is true about py/ Triangle J'K'L' shown on the grid below is a dilation of triangle JKL using the origin as the center of dilation 2345678910111 If angle A is congruent to itself by the Reflexive Property, which transformation could be used to prove AABC ~ AADE by AA similarity postulate? D m A Translate triangle ABC so that point C lies on point D to confirm LC = LD. Dilate AABC from point A by the ratio to confirm AD ~ AB AB Translate triangle ABC so that point B lies on point D to confirm ZB = LD. Dilate AABC from point A by the ratio AE to confirmSeth is using the figure shown below to prove the Pythagorean Theorem using triangle similarity: In the given triangle DEF, angle D is 90 and segment DG is perpendicular to segment EF. Part A: Identify a pair of similar triangles. (2 poinis) Part B: Explain how you know the triangles from Part A are similar. (4 points) Part C: If EG = 2 and EF = 8, find the length of segment ED. Show your work_ (4 points) The diagram below models the layout at a carnival where G, R, P, C, B, and E are various locations on the grounds. GRPC is a parallelogram. G R 350 ft 400 ft 300 ft B 200 ft P E Part A: Identify a pair of similar triangles. (2 points) Part B: Explain how you know the triangles from Part A are similar. (4 points) Part C: Find the distance from B to E and from P to E. Show your work. (4 points)