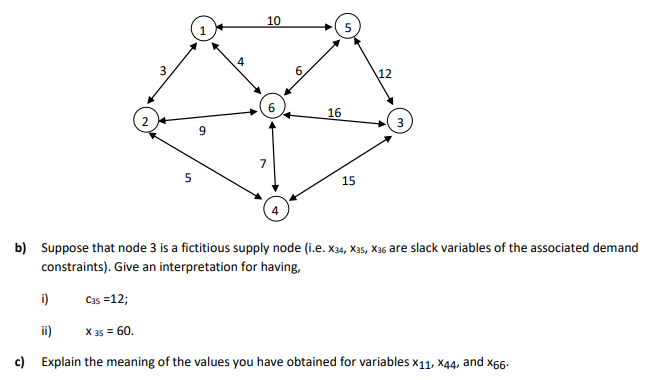
Question: there are three supply nodes and three demand nodes. Points 1, 2, 3 are the actual supply nodes with capacities 120, 80, 60 tons, respectively,

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


