There are two moment$-$area theorems. Theorem $1$ is used for finding the change in slope between two tangent lines, and Theorem $2$ is used for finding the vertical distance between two tangent lines. Below are the two moment$-$area theorems.

Theorem $1$: The change in slope between any two points on the elastic curve equals the area of the $\frac{M}{E}$ I diagram between these two points.

Considering $($Figure $1),$ the area under the MIEI diagram is ${}_{\frac{B}{A}}={\displaystyle \underset{A}{\overset{B}{}}}\frac{M}{EI}dx.$ The notation ${}_{\frac{B}{A}}$ is the angle of the tangent at $B$ measured with respect to the tangent at $A.$

Theorem $2$: The vertical deviation of the tangent at a point $(A)$ on the elastic curve with respect to the tangent extended from another point $(B)$ equals the "moment" of the area under the M$/$El diagram between the two points. This moment is computed about point $A($the point on

Figure

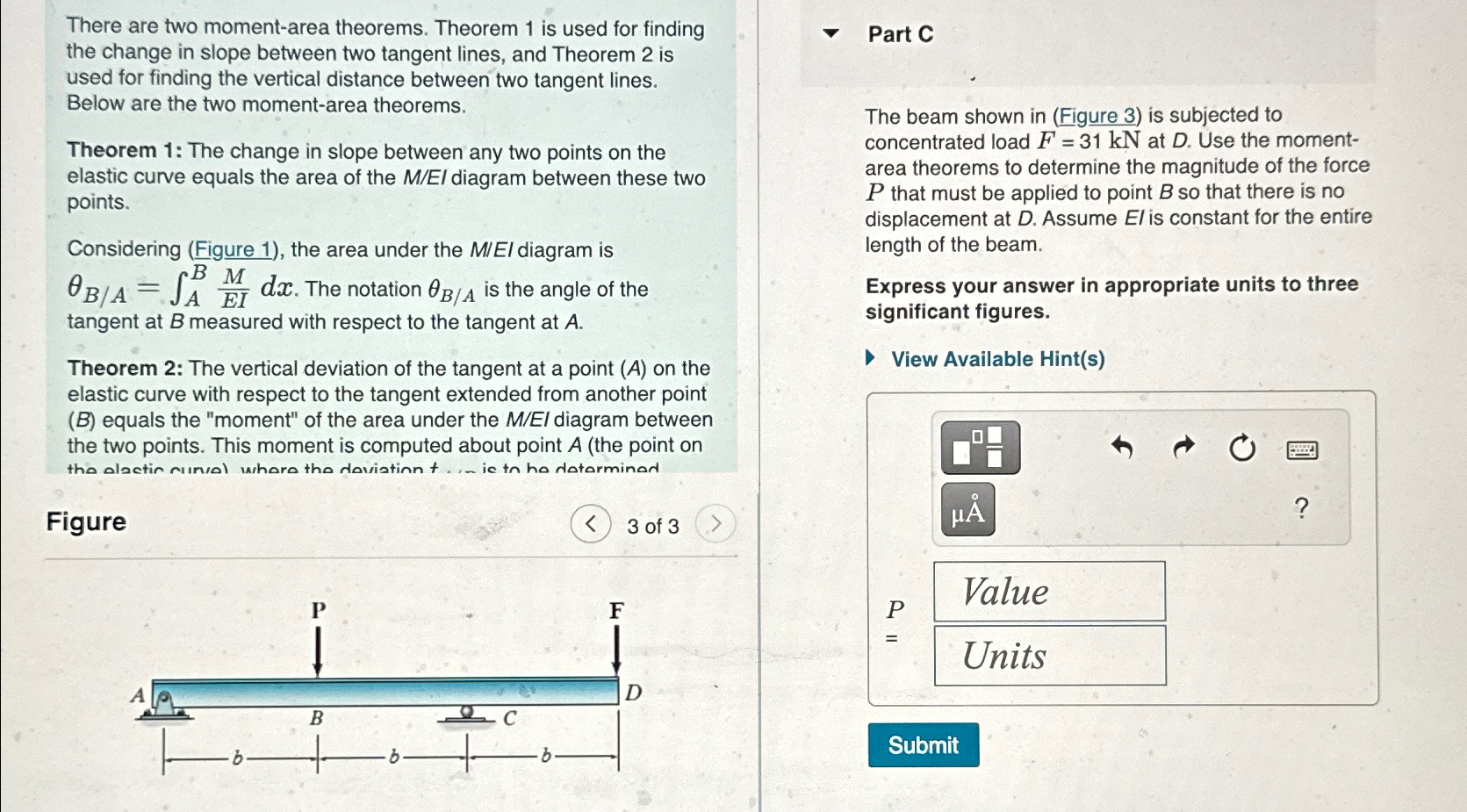
Part C

The beam shown in $($Figure $3)$ is subjected to concentrated load $F=31kN$ at $D.$ Use the momentarea theorems to determine the magnitude of the force $P$ that must be applied to point $B$ so that there is no displacement at $D.$ Assume $El$ is constant for the entire length of the beam.

Express your answer in appropriate units to three significant figures.

View Available Hint$($s$)$