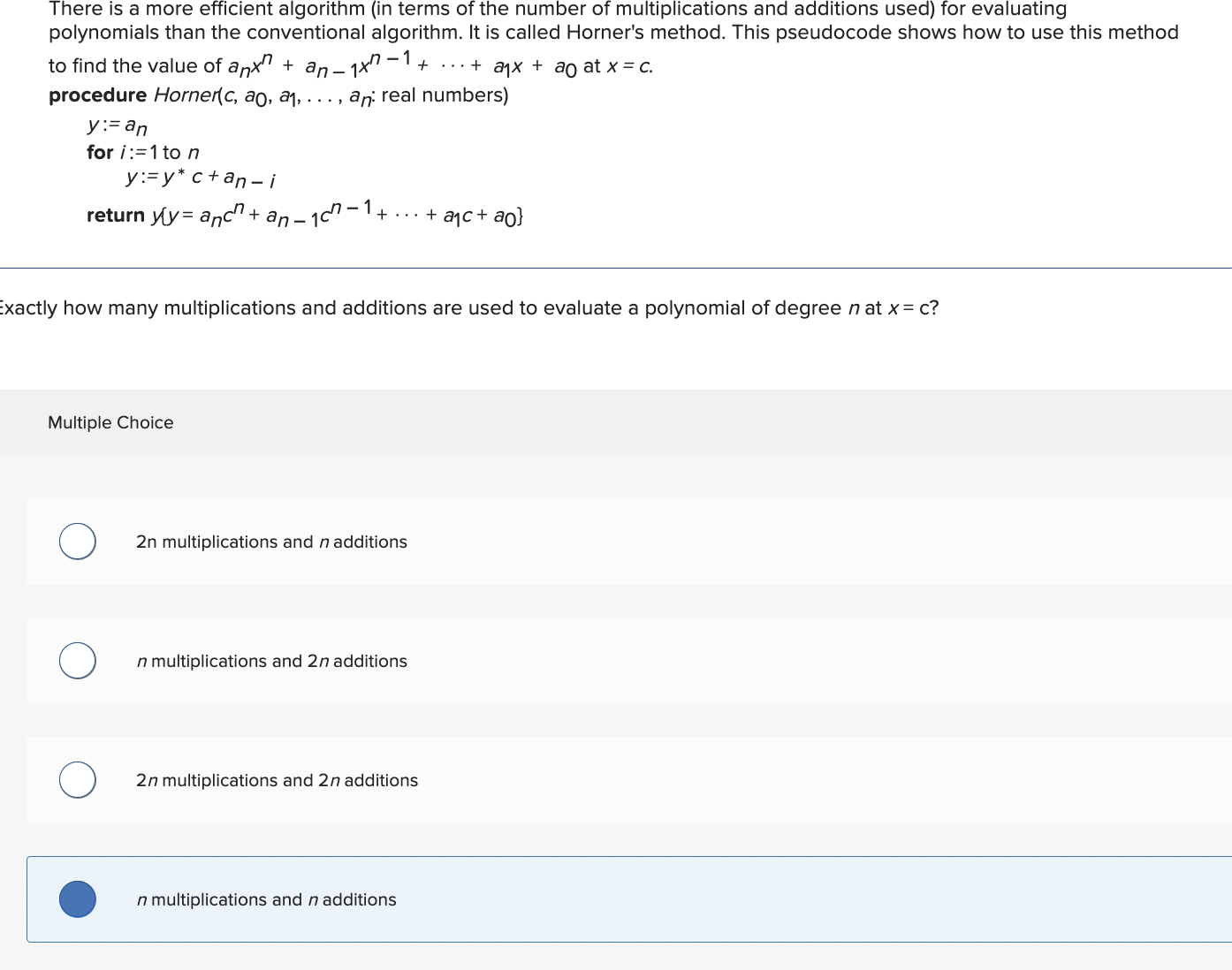
Question: There is a more efficient algorithm ( in terms of the number of multiplications and additions used ) for evaluating polynomials than the conventional algorithm.
There is a more efficient algorithm in terms of the number of multiplications and additions used for evaluating
polynomials than the conventional algorithm. It is called Horner's method. This pseudocode shows how to use this method
to find the value of cdots at
procedure Hornerdots, : real numbers
:
for :
:
return cdots
Exactly how many multiplications and additions are used to evaluate a polynomial of degree at
Multiple Choice
n multiplications and additions
multiplications and additions
multiplications and additions
multiplications and additions
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


