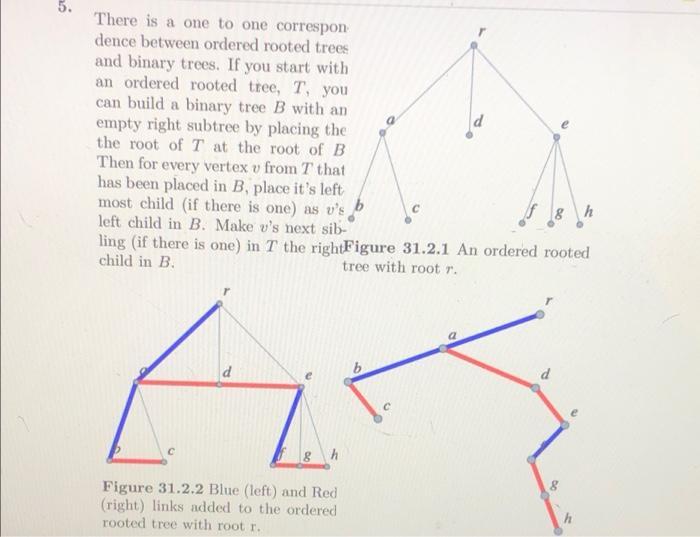
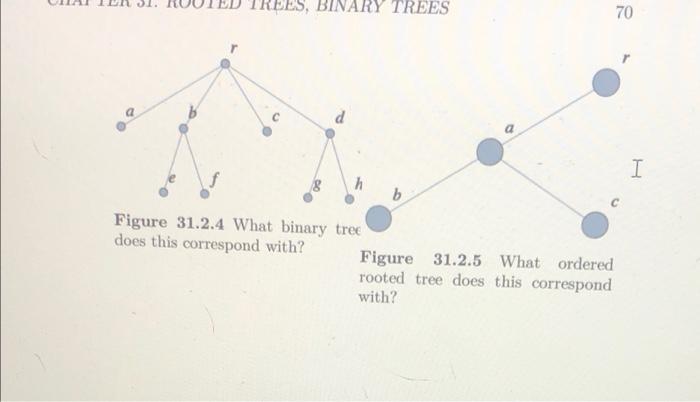
There is a one to one correspon dence between ordered rooted trees and binary trees. If you start with an ordered rooted tree, T, you can build a binary tree B with an empty right subtree by placing the the root of T at the root of B Then for every vertex v from T that has been placed in B, place it's left most child (if there is one) as v's left child in B. Make v's next sib- ling (if there is one) in T the rightFigure 31.2.1 An ordered rooted child in B. tree with root r. 8 h Figure 31.2.2 Blue (left) and Red (right) links added to the ordered rooted tree with root r. b (right) links added to the ordered rooted tree with root r. Th Figure 31.2.3 Binary tree cor- responding to the ordered rooted tree. (a) Why will B have no right children in this correspondence? (b) Draw the binary tree that is produced by the ordered rooted tree in Figure 31.2.4. (c) Draw the ordered tree that produces the binary tree in Fig- ure 31.2.5. (d) The left subtree of the binary tree in Figure 31.2.5 is one of 5 different binary trees with three vertices. Draw each of them and also the ordered rooted tree that each corresponds with. (e) What does this correspondence tell us about how the numbers of different binary trees and ordered rooted trees are related? TREES, BINARY TREES CO 180 Figure 31.2.4 What binary tree does this correspond with? b Figure 31.2.5 What ordered rooted tree does this correspond with? 70 I