These are given from my calculus class.

Please show all steps for section 1 and section 2, and section 3.

Thank you for your help.

You will make an optimal beverage can for this challenge.

Challenge:

Beverage cans are made from aluminum. The executives of the soda industry are searching at all possible cost-cutting steps because of the rising costs. To reduce costs as much as possible, you are asked to find a way to reinvent the conventional can. The manufacturer fills the containers with 355 cm³ of liquid and leaves 15 cm³ of open space, so it is important to maintain a total volume of 370 cm³.

Section 1: Creating a design of the can

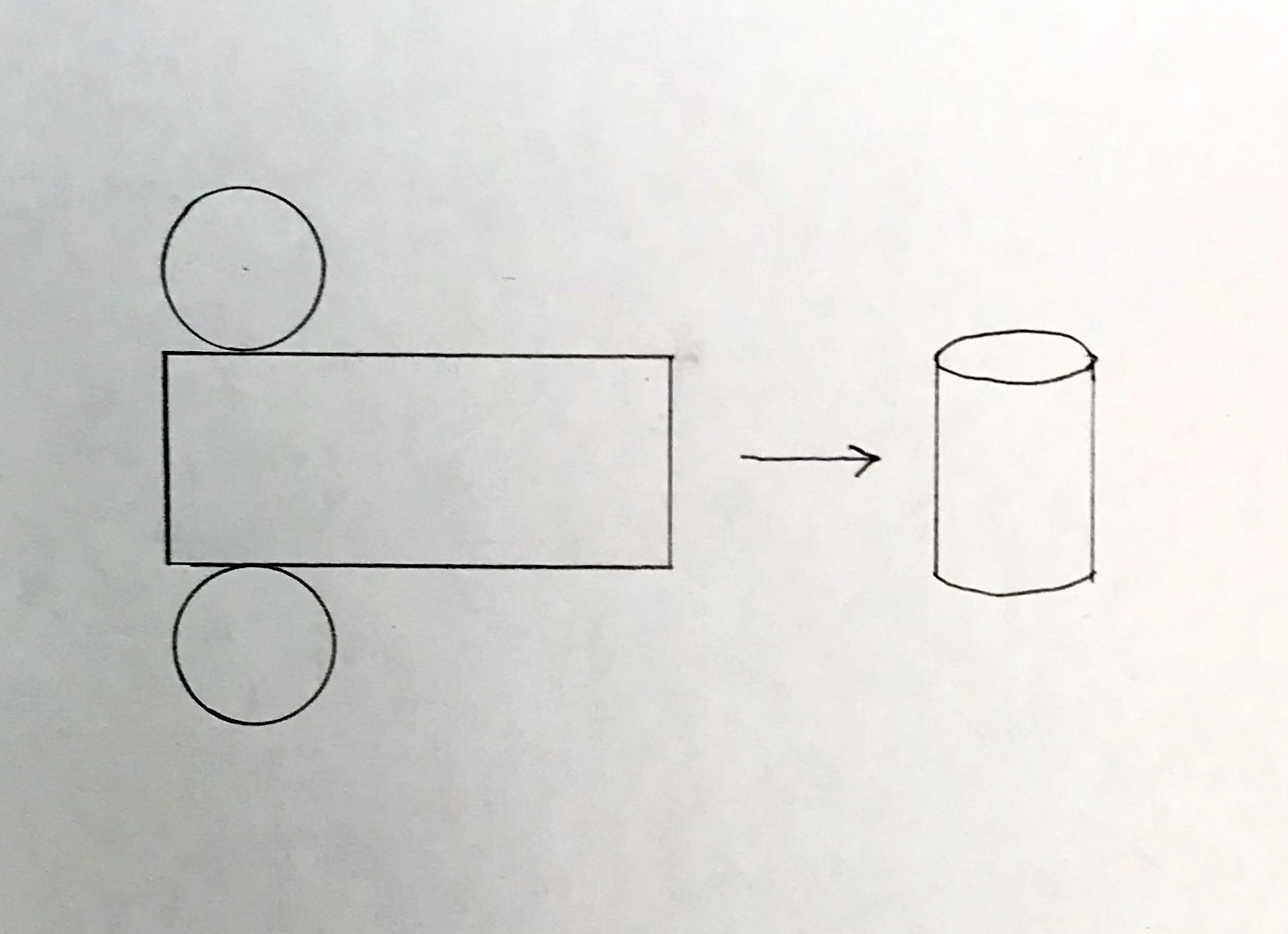
(1.) Draw a right circular cylinder and mark the radius, r, and height, h. Offer the volume and surface area formulas of a right circular cylinder. What quantity is known? Take and provide a picture of your drawing.

(2.) The objective is to minimize the area of the surface to maintain costs to a minimum, but consider that there are so many variables in the formula.

(2-A.) To remove height from the surface area formula, use the information in (1.) so that you only have surface area as a function of radius. Show your work here.

(2-B.) Use your work in (2-A). What is the realistic domain of surface area function that you generated?

(2-C.) Graph the surface area function in Desmos. Label each axis by name and units respectively. Include your graph with an image or drawing.

(3.) You have been working over intervals to find minimums and maximums of functions.

(3-A.) For estimating the value of the radius for which the surface area is least, referring to the graph from (2-C.) and use desmos. What is that radius, to the nearest hundredth, and what is the corresponding surface area, to the nearest hundredth? Don't forget units.

• Radius =
• Surface Area =

(3-B.) Please use calculus now. Evaluate the derivative of the surface area function and use the derivative to find the minimum surface area. Show your work.

(3-C.) Can you get the same value for the radius as in (3-A.) and (3-B.)? Will the values be the same?

(4.) Decide the corresponding dimensions for the radius that generates the minimum surface area. Round it up to the nearest hundredth. Show your work.

• Radius =
• Diameter =
• Height =

(5.) For making a paper three-dimensional beverage can, use the dimensions you have determined in (4.). As shown below, you can use a rectangle and two circles. Draw them to scale using a straightedge and compass if you have them. Show your drawing here.

\fOptimal Optimal Non - Reinforced Reinforced Can (Section 1 can ) Can (Section2 ) Diameter Height Surface area Volume