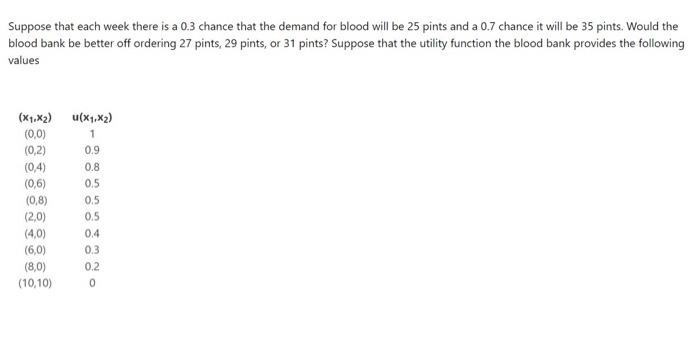this 2 parts from same question solve it with steps please

A blood bank must determine at the beginning of each week how many pints of blood should be ordered. Any blood left over at the end of the week spoils (it is outdated). For the blood bank, two attributes of interest are as follows: Attribute 1: Number of pints of blood by which ordered blood falls short of the week's demand (the weekly shortage). The weekly shortage is known to be always between 0 and 10 pints, Attribute 2: Number of pints of blood that are outdated (known to be always between 0 and 10 pints). Assume that attributes 1 and 2 exhibit mui. (a) Suppose the blood bank is indifferent between Option 1: Having a zero shortage and 10 outdated pints of blood Option 2: 83% of having 10 shortage and 10 outdated pints of blood, and 17% chance of having zero shortage and zero outdated pints of blood and between Option 3: Having a 10 shortage and zero outdated pints of blood Option 4: 32% of having 10 shortage and 10 outdated pints of blood, and 68% chance of having zero shortage and zero outdated pints of blood Express the blood bank's utility function in terms of u1(x1) and u2(x2). Suppose that each week there is a 0.3 chance that the demand for blood will be 25 pints and a 0.7 chance it will be 35 pints. Would the blood bank be better off ordering 27 pints, 29 pints, or 31 pints? Suppose that the utility function the blood bank provides the following values (X4,X2) 1 0.9 0.8 0.5 (X1.X2) (0,0) (0,2) (0,4) (0,6) (0,8) (2.0) (4,0) (6,0) (8,0) (10,10) 0.5 0.5 0.4 0.3 02 0 A blood bank must determine at the beginning of each week how many pints of blood should be ordered. Any blood left over at the end of the week spoils (it is outdated). For the blood bank, two attributes of interest are as follows: Attribute 1: Number of pints of blood by which ordered blood falls short of the week's demand (the weekly shortage). The weekly shortage is known to be always between 0 and 10 pints, Attribute 2: Number of pints of blood that are outdated (known to be always between 0 and 10 pints). Assume that attributes 1 and 2 exhibit mui. (a) Suppose the blood bank is indifferent between Option 1: Having a zero shortage and 10 outdated pints of blood Option 2: 83% of having 10 shortage and 10 outdated pints of blood, and 17% chance of having zero shortage and zero outdated pints of blood and between Option 3: Having a 10 shortage and zero outdated pints of blood Option 4: 32% of having 10 shortage and 10 outdated pints of blood, and 68% chance of having zero shortage and zero outdated pints of blood Express the blood bank's utility function in terms of u1(x1) and u2(x2). Suppose that each week there is a 0.3 chance that the demand for blood will be 25 pints and a 0.7 chance it will be 35 pints. Would the blood bank be better off ordering 27 pints, 29 pints, or 31 pints? Suppose that the utility function the blood bank provides the following values (X4,X2) 1 0.9 0.8 0.5 (X1.X2) (0,0) (0,2) (0,4) (0,6) (0,8) (2.0) (4,0) (6,0) (8,0) (10,10) 0.5 0.5 0.4 0.3 02 0