This data set is a subset of a larger experiment; we are using data from only one of the two alloys originally included in the experiment. Our data set will be used to analyze the effects of three factors (Method, Temperature, and Dentist) on the hardness of dental fillings. Each of five dentists prepared the gold alloy by each of the three methods of condensation and at each of the three temperatures used in the molting process. The dentist prepared a filling in an artificial substrate from each alloy made, and the hardness was measured via the Vickers Hardness Test. Note the resulting data set contains 45 observations, one for each treatment combination.

Read the data set into R. The levels of each of the three factors are numerically coded, so they will have to be declared as factors prior to subsequent analysis. Prior to declaring Temperature as a factor, save a copy of this variable as a numeric variable (e.g, Temp.Numeric

(a) Refer to the handout "Model Equations for Some Basic Experimental Designs". Try

implementing an analysis based on equation (6): the aov() model statement would be

Hardness ~ Method*Temperature*Dentist. You should encounter a problem with the analysis. What problem do you encounter?

(b)To deal with the previous problem, we will assume no three-factor interaction is present. This allows us to base our analysis on equation (7). There are a couple of ways of implementing this model in R. To be as brief as possible, if we have factors A, B, and C

and response variable Y, we could code the model in R by Y ~ A + B + C + A:B+ A:C + B:C. An efficient (but not obvious) way to generate the same model is Y ~(A + B + C)^2.

Substituting your variable names run this analysis and save the resulting

ANOVA table. (Note: You want to save tables output in R in a monospaced font, such as Courier New, otherwise numbers in columns won't line up properly and your output will look like crap).

(c) Recall that R automatically treats all factors as being fixed effects factors. If we were to treat all factors as fixed effects factors, what conclusions would you draw from the

ANOVA table? We are looking for a brief summary.

(d) There is a good argument that Dentist would be better considered as a random effects factor. What would we be assuming if we did so?

(e) If we consider Dentist as a random effects factor, what adjustments need to be made to the ANOVA table? Be precise; we are looking for changes in F-ratios (specify how these are calculated) and associated p-values.

(f) Do the conclusions change as a result of treating Dentists as a random effects factor? If so, how?

(g) You should have found one significant two-factor interaction. Prepare two side-by- side or top/bottom interaction plots that illustrate the nature of this interaction (these will look best if you expand the side-by-side plots to "full screen" before saving the pdf). What

appears to be the cause of the interaction?

(h) On the basis of the analysis conducted what recommendation should you make regarding preparing the dental gold alloy for fillings, and why?

(i) The effect (or lack of effect) of temperature on hardness can be examined graphically

use the plot(Y ~ X) command, substituting Hardness as the response variable and

Temperature as the predictor variable. How does the graphical output differ if Temperature is declared as a factor, in comparison to if Temperature is treated as a

numeric variable (previously stored as Temp.Numeric)?How would you describe the effect of Temperature on Hardness?

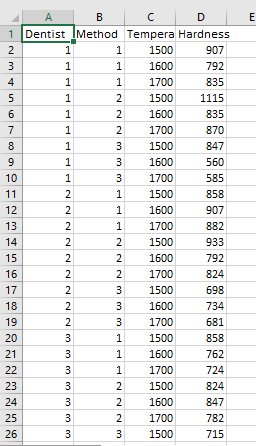
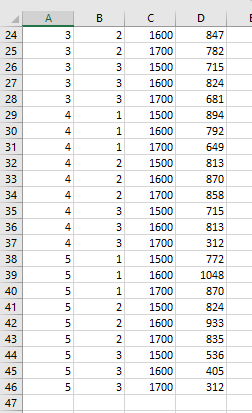
A B C D E Dentist IMethod Tempera Hardness 2 1 1500 907 1 1600 792 4 1 1700 835 1 2 1500 1115 1 2 1600 835 1700 870 1 1500 847 9 1 1600 560 10 1 1700 585 11 2 1500 858 12 2 1600 907 13 2 1700 882 14 2 O N N N KP 1500 933 15 2 1600 792 16 2 1700 824 17 1500 698 18 1600 734 19 2 1700 681 20 3 1500 858 21 LO 1600 762 22 3 1700 724 23 3 2 1500 824 24 3 2 1600 847 25 3 2 1700 782 26 3 3 1500 715A B C D 24 3 2 1600 847 25 3 2 1700 782 26 3 3 1500 715 27 3 1600 824 28 3 3 1700 681 29 A 1500 894 30 A 1600 764 31 1700 649 32 A 1500 813 33 1600 870 34 1700 858 35 3 1500 715 36 A 3 1600 813 37 3 1700 312 38 5 1500 772 39 5 1600 1048 40 5 1 1700 870 41 5 2 1500 824 42 5 2 1600 933 43 5 2 1700 835 44 5 3 1500 536 45 5 3 1600 405 46 5 3 1700 312 47(6) CRD with three treatment factors (axbxc factorial, n (=r) experimental units per treatment): YUH = 1 + a, + B; + yx + (ap), + (or), + (BY), + (aBY) + ETH; i =1,...,a; j = 1,...,b;k =1,...,c;/=1, ...,n (7) CRD with three treatment factors (axbxc factorial, one experimental unit per treatment, assume no ABC interaction): Yuk = 1 + a, + B, + 1x + (ap), + (ap) + (BY); + Egk; i = 1,...,a, j =1,..., b; k = 1, ...,c