this has been answered incorrectly multiple times

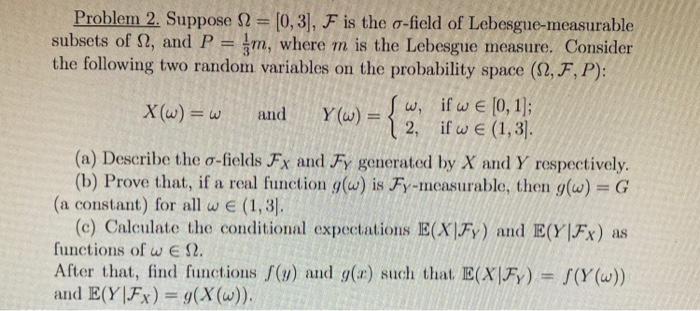
Problem 2. Suppose Q2 = (0,3), F is the o-field of Lebesgue-measurable subsets of 12, and P fm, where m is the Lebesgue measure. Consider the following two random variables on the probability space (S2, F,P): X(w)=w , and Y(w) = { if we (1,3) (a) Describe the o-fields Fx and Fy generated by X and Y respectively. (b) Prove that, if a real function g(w) is Fy-measurable, then g(w)=G (a constant) for all w (1,3). (c) Calculate the conditional expectations E(X)Fy) and E(Y|Fx) as functions of w ES2. After that, find functions /(y) and 9) such that E(X|Fy) = (Y(w)) and E(Y|Fx) = g(X(w))