This is a algorithms problem. If you are not clear about the problem, please give specifics on what needs clarification; don't put statements such as "not clear" or "needs more info", be specific. Please provide the answer typed out and written in python. Read the Context portion of the problem for more information.

Context Portion:

You can use the code below to generate a random graph with red nodes.

In the network below with 10 nodes, edge probability 0.3, color probability 0.5, and random seed set to 2021, we can create a network that has 1 red triangle, containing nodes: 3, 6, and 7.

Code to generate graph:

import networkx as nx import random def randomly_colored_graph(n, edge_prob, color_prob, seed): random.seed(seed) G = nx.Graph() for i in range(n): if random.random()

def draw_graph(G): nx.draw(G, with_labels=True, node_color=[ G.nodes[i]['color'] for i in G.nodes ])

#Function Call

a_network = randomly_colored_graph(10, edge_prob=0.3, color_prob=0.5, seed=2021) draw_graph(a_network)

Output from code above:

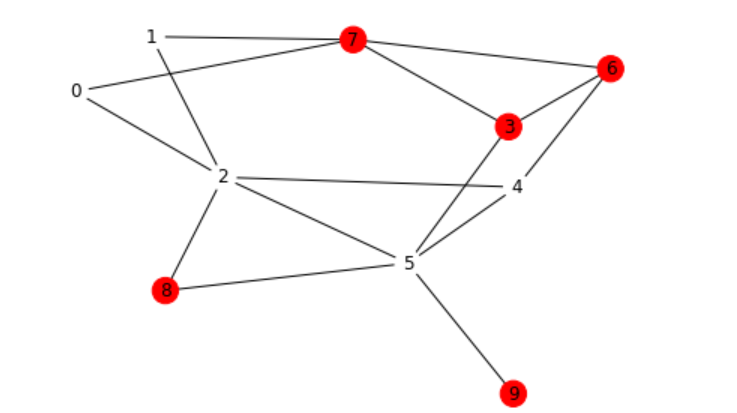
Functions(part of Context portion):

1)

def is_triangle(selection, network): nodes_selected = [] for i in range(len(selection)): if selection[i]: nodes_selected.append(i) if len(nodes_selected) != 3: return False has_edge = True for i in range(3): j = (i + 1)%3 has_edge = has_edge and network.has_edge(nodes_selected[i],nodes_selected[j]) return has_edge

2)

def is_red_triangle(selection, network): nodes_selected = [] for i in range(len(selection)): if selection[i]: nodes_selected.append(i) if len(nodes_selected) != 3: return False has_edge = True for i in range(3): color = network.nodes[nodes_selected[i]]['color'] if color != 'red': return False j = (i + 1)%3 has_edge = has_edge and network.has_edge(nodes_selected[i],nodes_selected[j]) return has_edge

Problem:

Complete/Modify the backtrack function below to find (print) all red triangles in a network.

def find_red_triangles(network): def backtrack(i): if i==len(selection): print(selection) else: for option in range(network): if is_red_triangle(selection, i): selection[i] = option backtrack(i+1) n = len(network.nodes) selection = [None] * n backtrack(0)

1 2 5 8 9 1 2 5 8 9