This is a game theory problem. Need help answering it.

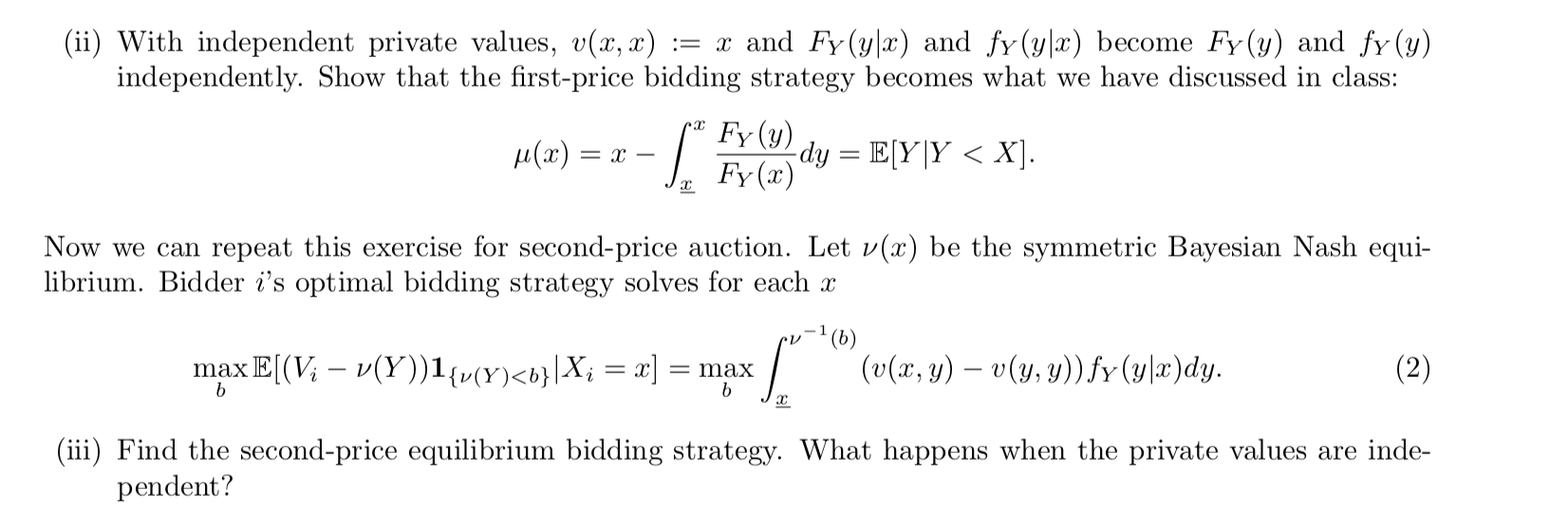
Problem 1 (Auctions with Interdependent Valuations). Consider bidder N bidders bidding for a single indivisible good. Bidder i observes a private signal X; that is informative about his value of the object, with X = (X1, X2, . . . , XN). The vector S = (S1, S2, . . ., SM) includes additional random variables that may be informative about the value of the object. Bidder i's value is Vi = ui(S, X). We can assume that ui(., .) is symmetric across i in that there is a function u(., .) on RM+N such that for all i, u; (S, X ) = u(S, Xi, {Xj}j+i). It means that all bidders' valuations depend on S in the same manner and each bidder's valuation is a symmetric function of the other bidders' signals. In class, we have discussed the case where M = 0 and Vi = ui(Xi), which is called the pure independent-private-value model. When Vi = ui(S), it is called common-value model as the valuations all depend on the random vector S. We assume that the bidders are risk-neutral. If bidder i wins the auction and pays price p for the object, his payoff is Vi - p. Denote Y as the highest signal among bidders other than i. It has cdf, Fy(y|x), and pdf, fy (y x ), conditioned on the realization x of Xi. In class, we have discussed the case where the signals are independent, then Fy (y|x), and pdf, fy (y|x) become Fy (y) and fy (y), respectively. We also define the expected value conditioned on the winning as v(x, y) := E[Vi|X; = x, Y = y] and the the expected value r(x) := E[Vi|Xi = x]. These two functions are symmetric across i so the indices i of v and r are dropped. Under this formulation, we can revisit the first price auction and aim to find symmetric Bayesian Nash equilibrium u(x). Here, we assume that u(x) is increasing and and u-I(x) exists. In a first-price auction, bidder i's optimal bidding strategy solves max E[(Vi - a)1{u(Y)