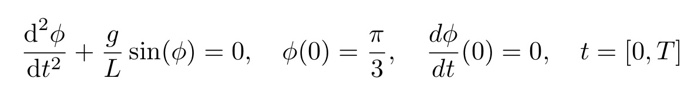this is a matlab-question. please do now answer if you are not sure on how to do it correct.

I need help to animate the swing of an pendulum. The animation can be made with the following code:

function anim (tout, fi, L)

for i=1:length(tout)-1

x0= L*sin(fi(i)); y0=-L*cos(fi(i));

plot ([0, x0] , [0,y0], '-o')

axis ('equal')

axis ([-1 1 -1 0]*1.2*L)

drawnow

pause(tout(i+1)-tout(i))

end;

end

L=length of the pendulum= 4 m

tout= is the times at which I, with Runge-Kutta4, have calculated the solution (see code below)

fi= calculated angel at the corresponding time

these values can be found using the following Matlab-code for the pendulum, but my problem is that I dont know how to use the following code, so I can find the values fi and tout so I can do the animation.

format long

L=4;

g=9.82;

f=@(t,y) [y(2),-(g*sin(y(1)))/L];

[x,y]=runge4(f,[0,10],[pi/3;0],0.1);

plot(x,y);

legend('angel','angular velocity');

function [x,y]=runge4(f,tspan,y0,h)

x = tspan(1):h:tspan(2);

y = zeros(length(x),2);

y(1,:) = y0;

for i=1:(length(x)-1)

k_1 = f(x(i),y(i,:));

k_2 = f(x(i)+0.5*h,y(i,:)+0.5*h*k_1);

k_3 = f((x(i)+0.5*h),(y(i,:)+0.5*h*k_2));

k_4 = f((x(i)+h),(y(i,:)+k_3*h));

y(i+1,:) = y(i,:) + (1/6)*(k_1+2*k_2+2*k_3+k_4)*h;

end

end

the pendulum can be described with a differential equation (see picture). is the angel and is the angular velocity

det + sin(a) = 0, 6(0) = el 10) = 0, += [0, 1] 2012 0, t= det + sin(a) = 0, 6(0) = el 10) = 0, += [0, 1] 2012 0, t=