This Is a question from my text book, it is from the chapter on Differential equations with Discontinuous Forcing Functions. It already solved with all the steps shown except it doesn't show the full work for Partial Fraction Expansion * see between steps 7 and 9. This is the work I did, obviously it is wrong. Please help me understand how they did the Partial Fraction Expansion.

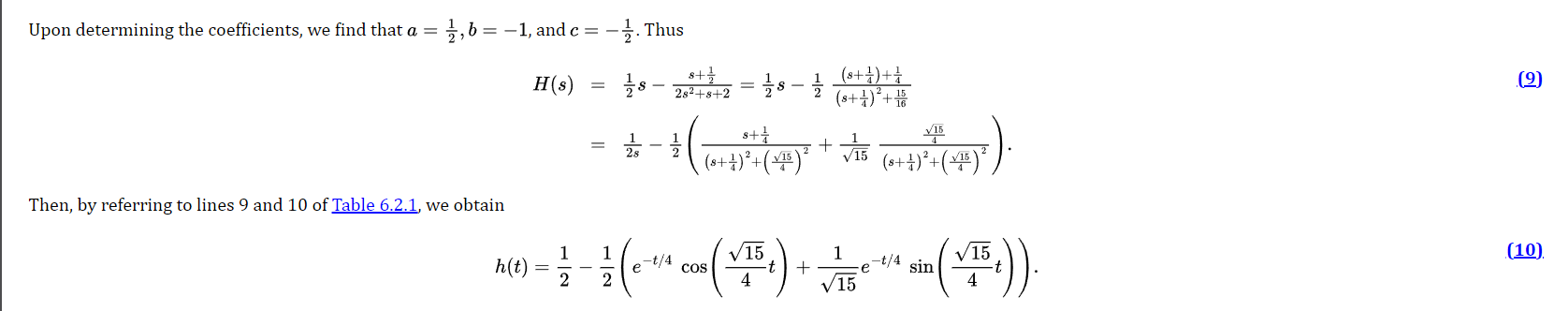
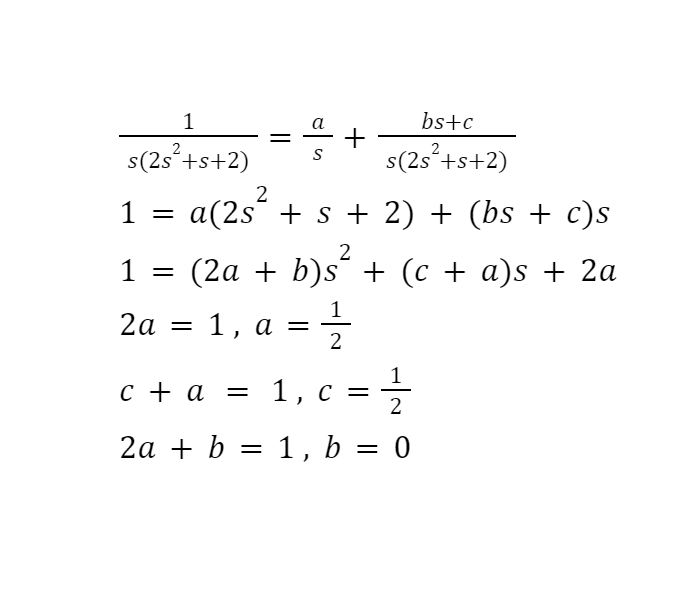
EXAMPLE 6.4.1 Find the solution of the differential equation 2y" +y' + 2y = g(t), (1). where 1, 5S t 20. (2). Assume that the initial conditions are y(0) = 0, y'(0) = 0. (3) This problem governs the charge on the capacitor in a simple electric circuit with a unit voltage pulse for 5 s t H(s) and e~ 205 H(5), respectively. Finally, to determine h(), we use the partial fraction expansion of H(s): a bs+c (8) H(s)=2 4 5 7 @ (s) 5+232+s+2 Upon determining the coefficients, we find that a = ?, b = -1, and c = - . Thus H (s) = 78 - - 78 - (s + 4 )+4 282+8+2 (8+ 4 ) 2 +18 (2) = 8+ 4 V15 28 (8+ +)? + (15 ) + V15 ( 8 + + ) ? + ( 215 ) 2 Then, by referring to lines 9 and 10 of Table 6.2.1, we obtain h (t) = e-t / 4 1 cos V15 + sin V15 e -t/4 (10). V15\f