This is a question from numerical analysis with matlab, can there some one help me correct the code I provided, thanks!(although the questions look so long, i believe you only need to change a little!)

The code provided:

https://drive.google.com/open?id=1zl2MIrcy5w8wORaVXjAvJ80XLyusJDp_

https://drive.google.com/open?id=1wyiTUosRDf7bR1zoCeXnKqVZoiD7Pvky

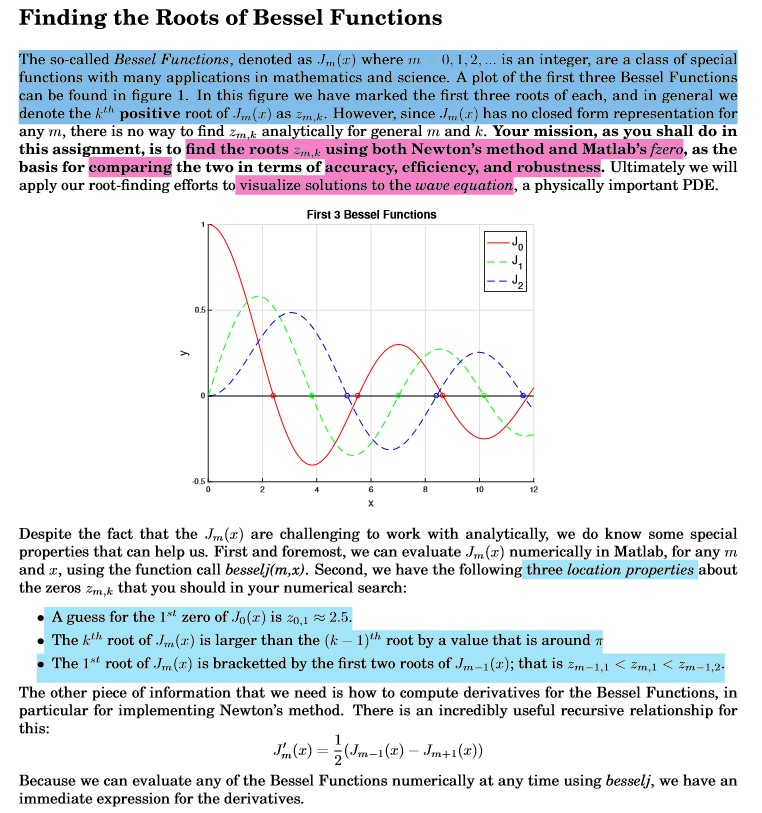
Finding the Roots of Bessel Functions The so-called Bessel Functions, denoted as () where functions with many applications in mathematics and science. A plot of the first three Bessel Functions can be found in figure 1. In this figure we have marked the first three roots of each, and in general we denote the kth positive root of .Im(r) as zm, k. However, since .Im(r) has no closed form representation for any m, there is no way to find zm,k analytically for general m and k. Your mission, as you shall do in this assignment, is to find the roots zm, using both Newton's method and Matlab's fzero, as the basis for comparing the two in terms of accuracy, efficiency, and robustness. Ultimately we will apply our root-finding efforts to visualize solutions to the wave equation, a physically important PDIE is an integer, are a class of specia , First 3 Bessel Functions 0.5 0.5 10 12 Despite the fact that the Jm(z) are challenging to work with analytically, we do know some special properties that can help us. First and foremost, we can evaluate Jm(x) numerically in Matlab, for any m and , using the function call bessel)(m,x). Second, we have the following three location properties about the zeros 2m,k that you should in your numerical search . A guess for the 1st zero of Jo(x) is z0,12.5. . The root of ./m(z) is larger than the (k-1)th root by a value that is around . The 1st root of J,n (r) is bracketted by the first two roots of '/m-1 (z); that is-m-1,1