This is a question on determining Volume.

Both the QUESTION and SOLUTION are shown below.

My Query is related to the resulting function, which the SOLUTION shows as correct , highlighted by a RED box, which is

(h+22d)(w+22d)=(h+d)(w+d)

Also,

(h+d)(w+d)=hw+hd+wd+d2

The equation I identified is

[(2d2)wh]2=2(dwh)

since I thought that Volume is height x width x depth.

Please explain how they identified the equation ?

Please explain clearly showing each step as thoroughly as possible. If you are using hand written notes, then please ensure they are neat and legible, as it is difficult to interpret illegible hand-written notes. Alternatively, use LaTex.

QUESTION

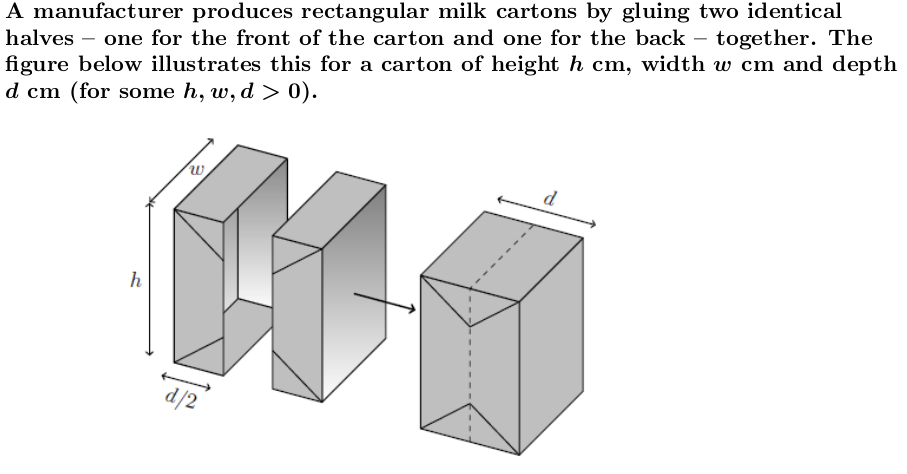
A manufacturer produces rectangular milk cartons by gluing two identical halves one for the front of the carton and one for the back together. The gure below illustrates this for a carton of height 1']; cm, width to cm and depth d cm (for some h, w,d > 0). The template used for both halves is shown below. To make each half, the corner squares of side d/2 are folded into a triangle (which can be seen in the previous illustration). We shall ignore any further overlapping material used for gluing. d/2 h d/2 d/2 W d/2 Suppose now that the manufacturer wants to minimise the material used to produce a carton subject to the constraint that its volume must be V. i. Formulating the manufacturer's optimisation problem as an equality constraint minimisation problem, explain why we can use the function f : R3 -> R defined by: f (h, w, d) = (h + d) (w +d) as our objective function.The total area for one half of a carton is: Therefore, the total area of material required to produce an entire carton is twice this. However, for our minimisation problem, we can ignore the constant, positive factor of 2 when writing the objective function