This is a simple project, but it will serve to demonstrate the approach. The following are the appropriate steps.

1.	Identify each activity to be done in the project and estimate how long it will take to complete each activity. This is simple, given the information from your instructor. We identify the activities as follows: A(1), B(2), C(1), D(1). The number is the expected duration of the activity.
2.	Determine the required sequence of activities and construct a network reflecting the precedence relationships. An easy way to do this is to first identify the immediate predecessors associated with an activity. The immediate predecessors are the activities that need to be completed immediately before an activity. Activity A needs to be completed before activities B and C can start. B and C need to be completed before D can start. The following table reflects what we know so far: Here is a diagram that depicts these precedence relationships:
3.	Page 145 Determine the critical path. Consider each sequence of activities that runs from the beginning to the end of the project. For our simple project there are two paths: ABD and ACD. The critical path is the path where the sum of the activity times is the longest. ABD has a duration of four weeks and ACD has a duration of three weeks. The critical path, therefore, is ABD. If any activity along the critical path is delayed, then the entire project will be delayed.
4.	Determine the early start/finish and late start/finish schedule. To schedule the project, find when each activity needs to start and when it needs to finish. For some activities in a project there may be some leeway in when an activity can start and finish. This is called the slack time in an activity. For each activity in the project, we calculate four points in time: the early start, early finish, late start, and late finish times. The early start and early finish are the earliest times that the activity can start and be finished. Similarly, the late start and late finish are the latest times the activities can start and finish without delaying the project. The difference between the late start time and early start time is the slack time. To help keep all of this straight, we place these numbers in special places around the nodes that represent each activity in our network diagram, as shown here. To calculate numbers, start from the beginning of the network and work to the end, calculating the early start and early finish numbers. Start counting with the current period, designated as period 0. Activity A has an early start of 0 and an early finish of 1. Activity B's early start is A's early finish or 1. Similarly, C's early start is 1. The early finish for B is 3, and the early finish for C is 2. Now consider activity D. D cannot start until both B and C are done. Because B cannot be done until 3, D cannot start until that time. The early start for D, therefore, is 3, and the early finish is 4. Our diagram now looks like this. To calculate the late finish and late start times, start from the end of the network and work toward the front. Consider activity D. The earliest that it can be done is at time 4; and if we do not want to delay the completion of the project, the late finish needs to be set to 4. With a duration of 1, the latest that D can start is 3. Now consider activity C. C must be done by time 3 so that D can start, so C's late finish time is 3 and its late start time is 2. Notice the difference between the early and late start and finish times: This activity has one week of slack time. Activity B must be done by time 3 so that D can start, so its late finish time is 3 and late start time is 1. There is no slack in B. Finally, activity A must be done so that B and C can start. Because B must start earlier than C, and A must get done in time for B to start, the late finish time for A is 1. Finally, the late start time for A is 0. Notice there is no slack in activities A, B, and D. The final network looks like this. (Hopefully the stock your investment team has chosen is a winner!)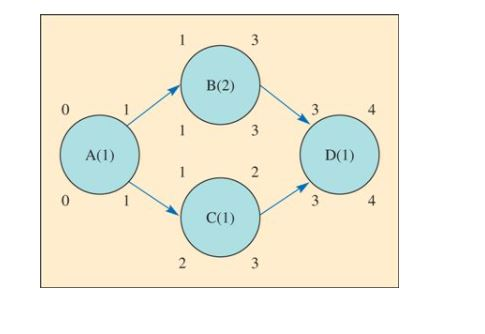

This is a simple project, but it will serve to demonstrate the approach. The following are the appropriate steps. 1. Identify each activity to be done in the project and estimate how long it will take to complete each activity. This is simple, given the information from your instructor. We identify the activities as follows: A(1), B(2), C(1), D(1). The number is the expected duration of the activity. 2. Determine the required sequence of activities and construct a network reflecting the precedence relationships. An easy way to do this is to first identify the immediate predecessors associated with an activity. The immediate predecessors are the activities that need to be completed immediately before an activity. Activity A needs to be completed before activities B and C can start. B and C need to be completed before D can start. The following table reflects what we know so far: DESIGNATION IMMEDIATE PREDECESSORS TIME (WEEKS) A None 1 ACTIVITY Select company Obtain annual report and perform ratio analysis Collect stock price data and perform technical analysis Review data and make a decision B 2 C A 1 D Bandc 1 Here is a diagram that depicts these precedence relationships: Report and Ratio Analysis B(2) Select Company Make Decision A(1) D(1) C(1) Technical Analysis Page 145etermine the critical path. Consider each sequence of activities that runs from the beginning to the end of the project. For our simple project there are two paths: A-B-D and A-C-D. The critical path is the path where the sum of the activity times is the longest. A-B-D has a duration of four weeks and A-C-D has a duration of three weeks. The critical path, therefore, is A-B-D. If any activity along the critical path is delayed, then the entire project will be delayed. 4. Determine the early start/finish and late start/finish schedule. To schedule the project, find when each activity needs to start and when it needs to finish. For some activities in a project there may be some leeway in when an activity can start and finish. This is called the slack time in an activity. For each activity in the project, we calculate four points in time: the early start, early finish, late start, and late finish times. The early start and early finish are the earliest times that the activity can start and be finished. Similarly, the late start and late finish are the latest times the activities can start and finish without delaying the project. The difference between the late start time and early start time is the slack time. To help keep all of this straight, we place these numbers in special places around the nodes that represent each activity in our network diagram, as shown here. Early start Early finish Activity (duration) Late start Late finish To calculate numbers, start from the beginning of the network and work to the end, calculating the early start and early finish numbers. Start counting with the current period, designated as period 0. Activity A has an early start of O and an early finish of 1. Activity B's early start is A's early finish or 1. Similarly, C's early start is 1. The early finish for B is 3, and the early finish for Cis 2. Now consider activity D. D cannot start until both B and C are done. Because B cannot be done until 3, D cannot start until that time. The early start for D, therefore, is 3, and the early finish is 4. Our diagram now looks like this. 3 B(2) 0 " 4 A(1) D(1) 2 2 C(1) To calculate the late finish and late start times, start from the end of the network and work toward the front. Consider activity D. The earliest that it can be done is at time 4, and if we do not want to delay the completion of the project, the late finish needs to be set to 4. With a duration of 1, the latest that D can start is 3. Now consider activity C. C must be done by time 3 so that D can start, so C's late finish time is 3 and its late start time is 2. Notice the difference between the early and late start and finish times: This activity has one week of slack time. Activity B must be done by time 3 so that D can start, so its late finish time is 3 and late start time is 1. There is no slack in B. Finally, activity A must be done so that B and C can start. Because B must start earlier than C, and A must get done in time for B to start, the late finish time for Ais 1. Finally, the late start time for A is 0. Notice there is no slack in activities A, B, and D. The final network looks like this. (Hopefully the stock your investment team has chosen is a winner!) 3 B(2) 3 4 3 A(1) D(1) 0 C(1) 2 3 This is a simple project, but it will serve to demonstrate the approach. The following are the appropriate steps. 1. Identify each activity to be done in the project and estimate how long it will take to complete each activity. This is simple, given the information from your instructor. We identify the activities as follows: A(1), B(2), C(1), D(1). The number is the expected duration of the activity. 2. Determine the required sequence of activities and construct a network reflecting the precedence relationships. An easy way to do this is to first identify the immediate predecessors associated with an activity. The immediate predecessors are the activities that need to be completed immediately before an activity. Activity A needs to be completed before activities B and C can start. B and C need to be completed before D can start. The following table reflects what we know so far: DESIGNATION IMMEDIATE PREDECESSORS TIME (WEEKS) A None 1 ACTIVITY Select company Obtain annual report and perform ratio analysis Collect stock price data and perform technical analysis Review data and make a decision B 2 C A 1 D Bandc 1 Here is a diagram that depicts these precedence relationships: Report and Ratio Analysis B(2) Select Company Make Decision A(1) D(1) C(1) Technical Analysis Page 145etermine the critical path. Consider each sequence of activities that runs from the beginning to the end of the project. For our simple project there are two paths: A-B-D and A-C-D. The critical path is the path where the sum of the activity times is the longest. A-B-D has a duration of four weeks and A-C-D has a duration of three weeks. The critical path, therefore, is A-B-D. If any activity along the critical path is delayed, then the entire project will be delayed. 4. Determine the early start/finish and late start/finish schedule. To schedule the project, find when each activity needs to start and when it needs to finish. For some activities in a project there may be some leeway in when an activity can start and finish. This is called the slack time in an activity. For each activity in the project, we calculate four points in time: the early start, early finish, late start, and late finish times. The early start and early finish are the earliest times that the activity can start and be finished. Similarly, the late start and late finish are the latest times the activities can start and finish without delaying the project. The difference between the late start time and early start time is the slack time. To help keep all of this straight, we place these numbers in special places around the nodes that represent each activity in our network diagram, as shown here. Early start Early finish Activity (duration) Late start Late finish To calculate numbers, start from the beginning of the network and work to the end, calculating the early start and early finish numbers. Start counting with the current period, designated as period 0. Activity A has an early start of O and an early finish of 1. Activity B's early start is A's early finish or 1. Similarly, C's early start is 1. The early finish for B is 3, and the early finish for Cis 2. Now consider activity D. D cannot start until both B and C are done. Because B cannot be done until 3, D cannot start until that time. The early start for D, therefore, is 3, and the early finish is 4. Our diagram now looks like this. 3 B(2) 0 " 4 A(1) D(1) 2 2 C(1) To calculate the late finish and late start times, start from the end of the network and work toward the front. Consider activity D. The earliest that it can be done is at time 4, and if we do not want to delay the completion of the project, the late finish needs to be set to 4. With a duration of 1, the latest that D can start is 3. Now consider activity C. C must be done by time 3 so that D can start, so C's late finish time is 3 and its late start time is 2. Notice the difference between the early and late start and finish times: This activity has one week of slack time. Activity B must be done by time 3 so that D can start, so its late finish time is 3 and late start time is 1. There is no slack in B. Finally, activity A must be done so that B and C can start. Because B must start earlier than C, and A must get done in time for B to start, the late finish time for Ais 1. Finally, the late start time for A is 0. Notice there is no slack in activities A, B, and D. The final network looks like this. (Hopefully the stock your investment team has chosen is a winner!) 3 B(2) 3 4 3 A(1) D(1) 0 C(1) 2 3