This is a UC Berkeley Prob 140 question please help I have to submit in 2 hours.

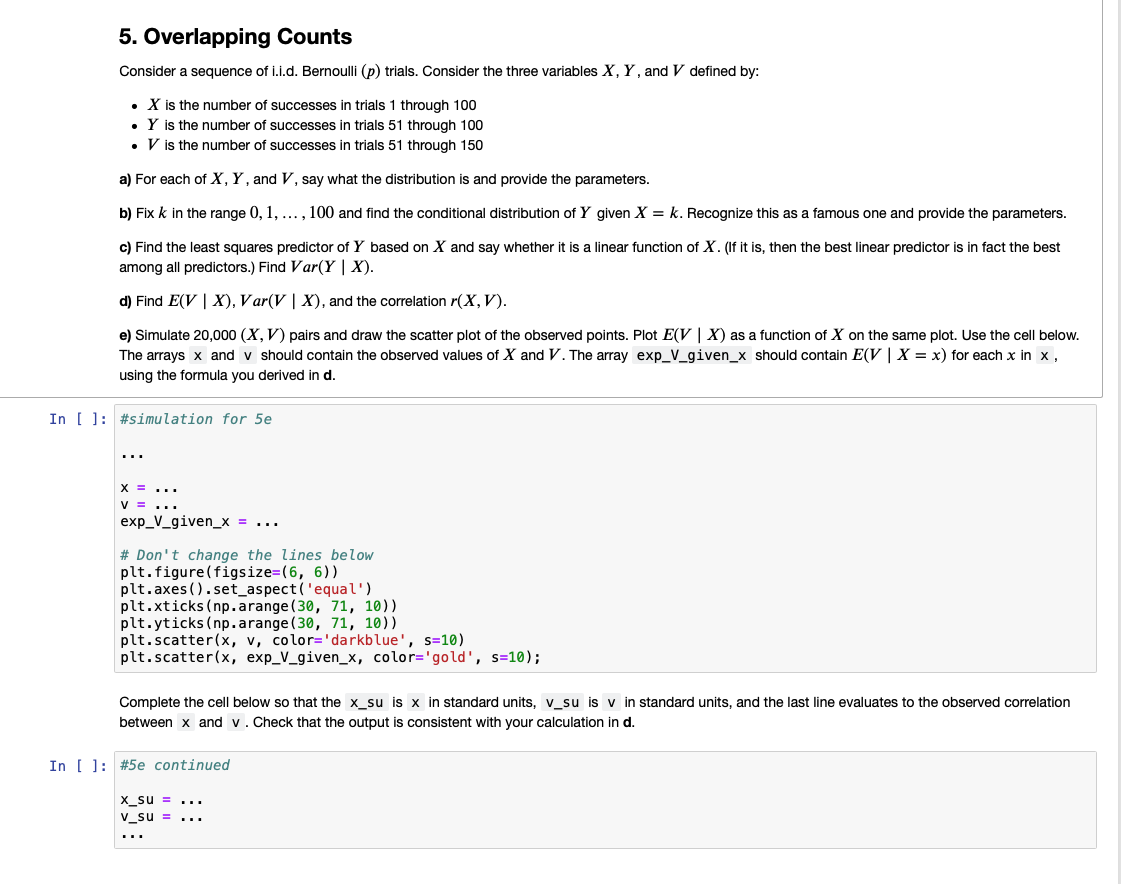
5. Overlapping Counts Consider a sequence of i.i.d. Bernoulli (p) trials. Consider the three variables X, Y , and I/ defined by: . X is the number of successes in trials 1 through 100 . Y is the number of successes in trials 51 through 100 V is the number of successes in trials 51 through 150 a) For each of X, Y , and I', say what the distribution is and provide the parameters. b) Fix k in the range 0, 1, ... , 100 and find the conditional distribution of Y given X = k. Recognize this as a famous one and provide the parameters. c) Find the least squares predictor of Y based on X and say whether it is a linear function of X. (If it is, then the best linear predictor is in fact the best among all predictors.) Find Var(Y | X). d) Find E(V | X), Var(V | X), and the correlation r(X, V). e) Simulate 20,000 (X, I') pairs and draw the scatter plot of the observed points. Plot E( | X) as a function of X on the same plot. Use the cell below. The arrays x and v should contain the observed values of X and I". The array exp_V_given_x should contain E(V | X = x) for each x in x , using the formula you derived in d. In [ ]: #simulation for 5e X = . . . V = . . . exp_V_given_x = . . . # Don't change the lines below plt . figure (figsize=(6, 6)) pit. axes ( ) . set_aspect ( 'equal' ) plt . xticks (np. arange (30, 71, 10)) plt . yticks (np. arange (30, 71, 10)) pit . scatter(x, v, color='darkblue' , s=10) plt . scatter(x, exp_V_given_x, color='gold', s=10); Complete the cell below so that the x_su is x in standard units, v_su is v in standard units, and the last line evaluates to the observed correlation between x and v . Check that the output is consistent with your calculation in d. In [ ]: #5e continued X_SU = . . . V_SU =