this is all the information please help me

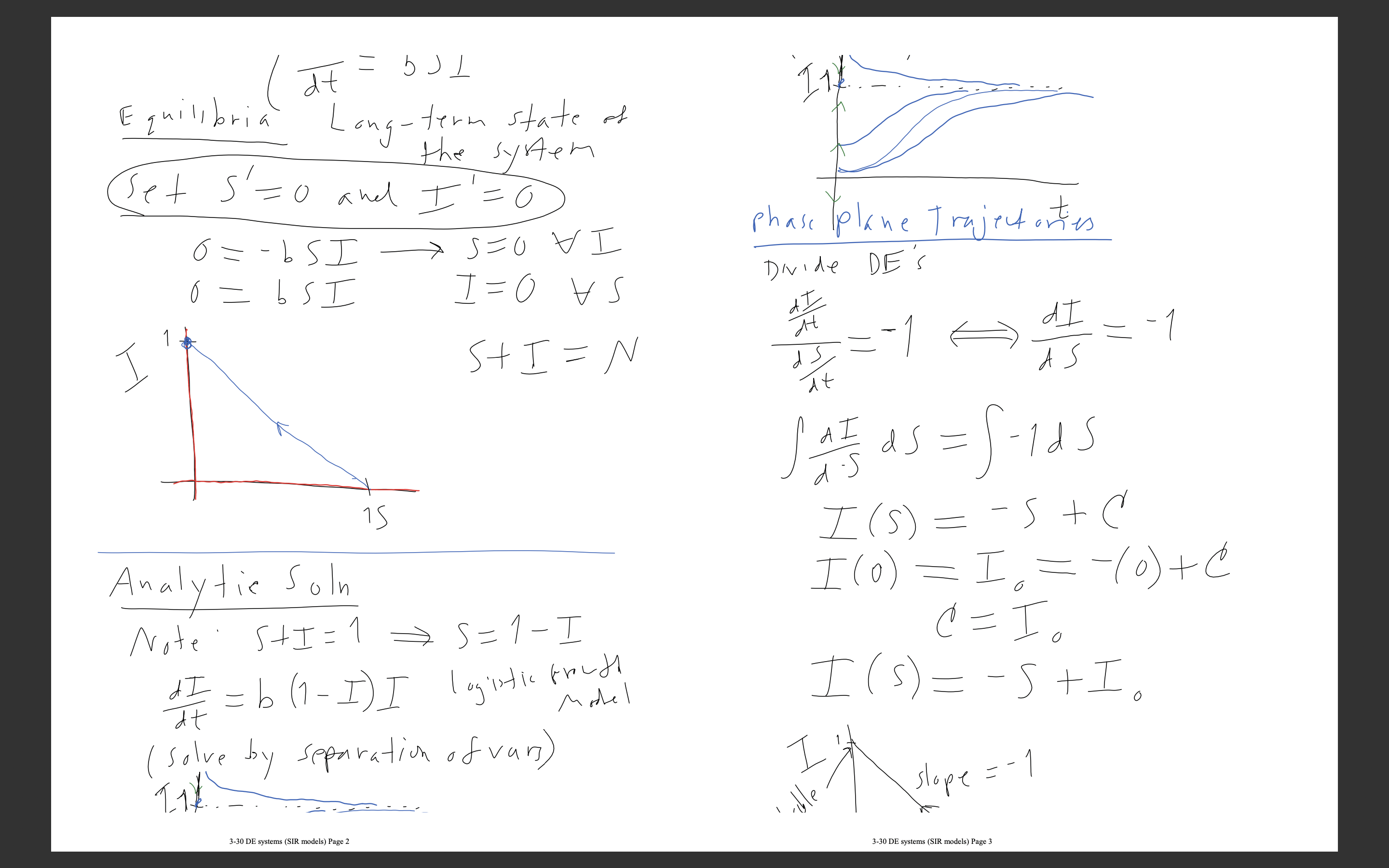
Find the nullclines and equilibrium points of the SIRS system. Using the SIR model, a. Derive the solution for I(S) from the SIR model. b. Derive the formula for R-naught involving 5* c. If the total number of people (in a population of size 100,000} who did not get infected by a virus by the end of an outbreak is 60,000, determine R-naught (using the formula from part b.). d. If the viral infection (from part c.) is contagious for a period of 4 days, determine the value of the parameter k. Use this value and the R-naught value to determine the contact rote. e. Find the minimum vaccination rate for this infectious disease. SIR models 1 Monday , March 30, 2020 1:04 PM systems of DE s Infections Disease Models ( SJR ) sit) to of susceptible Individuals at time t I ( t ) olb of infected R(t) olo of recovered N (t ) total pop N = S+ItR (assume constant ) N + N N SI Model I Let b # of contacts sufficient to transmit the virus per time per individual then by # of new infections pertime generated by a single infected individual the model is = - bs I At * I It = b SI 3-30 DE systems (SIR models) Page 1Equilibria Long-term state of the system Set S = O and I = O 6 = - b s I -> s zu VI phase plane Trajectonties 0 - bsI I = O V S Divide DE'S At S+ I = N - -1 d s AS at at as = 1 - Ids I ( s ) = - s + ( Analytic Soln I ( 0 ) = I . = - ( 0 ) + @ Note ' S t I = 1 => S = 1 - I C = I . d I = b ( 1 - I ) I logistic trough Model I ( s ) = - S + I . ( solve by separation of vary ) slope = - 1 3-30 DE systems (SIR models) Page 2 3-30 DE systems (SIR models) Page 3slope stable. I = Ous (unstable) 6 Un stadle S bS I ( - bstr ) = 0-7/st. 6 SIS Model S Since I = 1 -S, (I- 1-Y I b = 05 I rate of recover V = 0.2 ( loss of immunity ) r r fraction of infected group the) s* = b 6 2 - 0.4 05 recovers pertime SIS /R Model b 5 ' = - b s I tr I S I = b S I - r. I I E. g, If the any duration of infection M is 3days , then an average, Mortality , of the currently infected pop recovers each dry Heure r= 12 Eg- Values S ' = 0 = - b s I + rI I = 0 = bs I - vI 3-30 DE systems (SIR models) Page 4 3-30 DE systems (SIR models) Page 5