This is an advanced linear algebra course. (P_n(F))' denotes the dual for (P_n(F)) which is a n degree polynomial that takes in a number which could be real or complex.

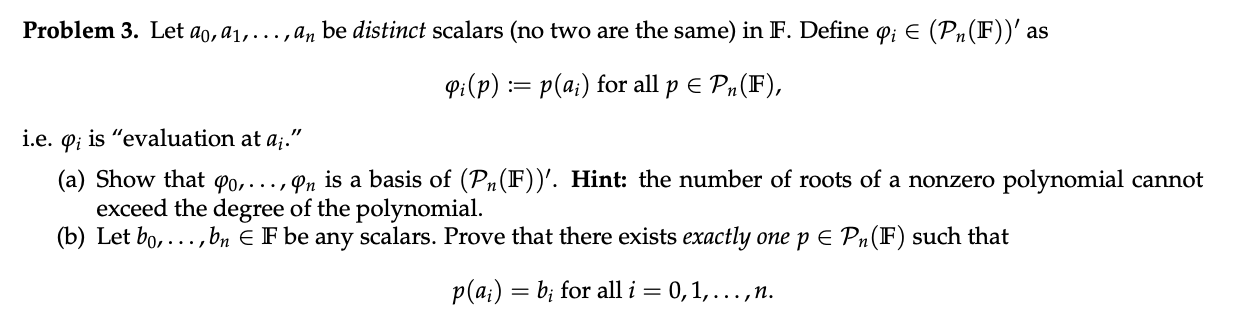
Problem 3. Let do, a1, . .., an be distinct scalars (no two are the same) in IF. Define q; E (Pn (IF) )' as pi(p) := p(ai) for all p E Pn(IF), i.e. q; is "evaluation at ai." (a) Show that Po, . .., On is a basis of (Pn (IF) )'. Hint: the number of roots of a nonzero polynomial cannot exceed the degree of the polynomial. (b) Let bo, . .., bn E IF be any scalars. Prove that there exists exactly one p E Pn(IF) such that p(ai) = b; for all i = 0, 1, ..., n