This is an exercise in implementing functions to solve a large problem. Some of the function specifications are already dictated by the assignment below, but a student is welcome to define any other functions that might be helpful in solving the problem.

There is a starter program file provided with this assignment (in the Functions Module) that predefines the names and interfaces of several functions in a suitable order in the file. A section later in this document will give a road map to that file to explain what will be filled in.

Assignment Description

This program will simulate part of the game of Yahtzee!

This is a dice game that involves rolling five dice and scoring points based on what show up on those five dice. The players would record their scores on a score card, and then total them up, and the player with the larger total wins the game.

A Yahtzee score card has two portions:

The upper portion has spaces for six scores, obtained by adding up all of the 1's, 2's, 3's, etc.

The lower portion has special scores for various combinations:

Three of a kind -- at least 3 dice are the same number; the score is the sum of all five dice

Four of a kind -- at least 4 dice are the same number; the score is the sum of all five dice

Small straight -- four consecutive numbers are represented, e.g. 2345; the score is 25 points

Large straight -- five consecutive numbers are represented, e.g. 23456; the score is 30 points

Full House -- three of one kind, two of another; the score is 30 points

Yahtzee! -- five of a kind; the score is 50 points

Chance -- nothing special; the score is the sum of all five dice

In a typical turn of this game, a players take rolls five dice, and then has two opportunities to reroll any dice that are desired, and then those dice are evaluated according to the options above.

To keep the assignment size manageable, the basic assignment will not need to represent the entire game. It will simply roll five dice and evaluate them, and then allow the player to roll another new set of five dice, and evaluate those. It will not need to keep score, either.

Here are some sample results from the instructor's solution. For readability, I put the upper and lower portions side by side.

Rolled: 6 6 4 4 4 Three of a Kind 24 Sets of 1's: 0 Four of a Kind 0 Sets of 2's: 0 Full House 30 Sets of 3's: 0 Small Straight 0 Sets of 4's: 12 Large Straight 0 Sets of 5's: 0 Yahtzee 0 Sets of 6's: 12 Chance 24 Another (y)? y Rolled: 2 2 6 6 1 Three of a Kind 0 Sets of 1's 1 Four of a Kind 0 Sets of 2's 4 Full House 0 Sets of 3's 0 Small Straight 0 Sets of 4's 0 Large Straight 0 Sets of 5's 0 Yahtzee 0 Sets of 6's 12 Chance 17 Another (y)? y Rolled: 3 5 2 5 4 Three of a Kind 0 Sets of 1's 0 Four of a Kind 0 Sets of 2's 2 Full House 0 Sets of 3's 3 Small Straight 25 Sets of 4's 4 Large Straight 0 Sets of 5's 10 Yahtzee 0 Sets of 6's 0 Chance 19 Another (y)? n 

THE CODE I HAVE SO FAR:

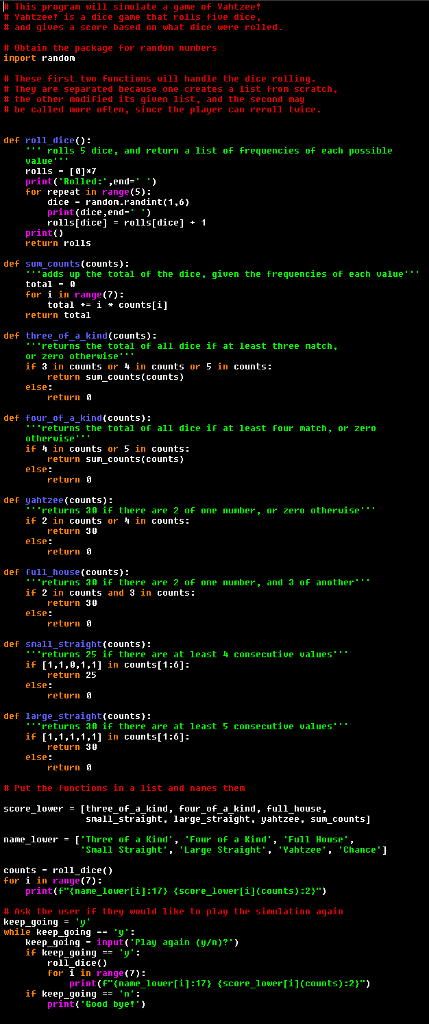
# This progran will sinu iate a game of Yahtzee? # Yahtzee? is a dice game that rolls flue dice # and gives a score based on what dice uere rolled # Obtain the package for randon nunbers inport randon # These first two functions uill handle the dice rolling # 1hey are separated because one creates a list fron scratch, # the ther nodified its giuen list, and the second may # be called more often, since the player can reroll tuice def roll1 dice: rolls 5 dice, and return a list of Frequencies of each possible value' rolls- [81*7 print( Rolled:,end-' ') for repeat in range(5) dice randon.randint 1,6) print(dice,end-) rolls(dice] = rolls[dice] + 1 print() return rolls def sumcounts(counts) adds up the total of the dice, given the frequencies of each value total -0 for i in range(7) return total total i countsti] def three of a_kind (counts): "returns the total of all dice if at least three natch, r zero other ise. if 3 in counts or in counts or 5 in counts: return sun counts(counts) else: return def fourof_a_kind counts): returns the total of all dice if at least Four match or zero otherwise if h in counts or 5in counts: return suncounts( counts - else: return 9 def yahtzee(counts): returns 30 if there are 2 of one nunber, or zero otheruise'"" if 2 in counts or in counts: return 30 else: return 9 def Ful1 house(counts): returns 30 if there are 2 of one nunber, and 3 of another if 2 in counts and 3 in counts: return 30 else: return def snall_straight (counts): returns 25 if there are at least consecutive values if [1,1,0,1,1] in counts[1:6]: return 25 else: return def large straight (counts): returns a0 if there are at least 5 consecutiue values if [1,1,1,1,1] in counts[1:]: return 30 else: return # Put the functions in a list and nanes then score-lower [three-of-a-kind, four of kind, full-house, = a snall straight. large straight, yahtzee, sum counts] name louer[Three of a Kind'Four of a Kind Snall Straight Large Straight. Fu11 House, Yahtzee. ' counts -roll dice) for i in range(7) print(f"nane_lower[i]:17score_lower[i] (counts):2" # Ask the user if they would like to play the sinulation again keep goingy while keep goingy keep going input( P1ay again (y)? ) if keep going- y roll dice) For i in range(7): print. (f..(name 1uer[1] :17) {score-Inwer[1](counts) :2)") if keep going - 'n print Good bye