This is for abstract algebra class. Please show me all the details from scratch. Thank you.

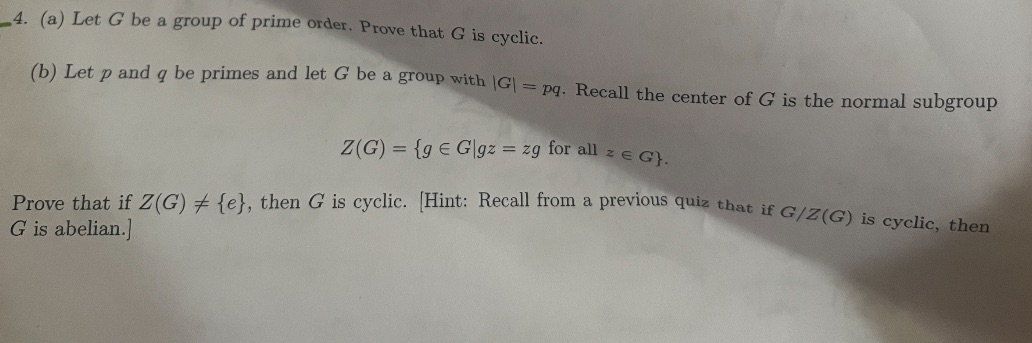
_4. (a) Let G be a group of prime order. Prove that G is cyclic. (b) Let p and q be primes and let G be a group with (G) = pq. Recall the center of G is the normal subgroup Z(G) = {g E G|gz = zg for all z e G}. Prove that if Z(G) # {el, then G is cyclic. [Hint: Recall from a previous quiz that if G/Z(G) is cyclic, then G is abelian.]