This is how the excel document should begin before answering the questions above:

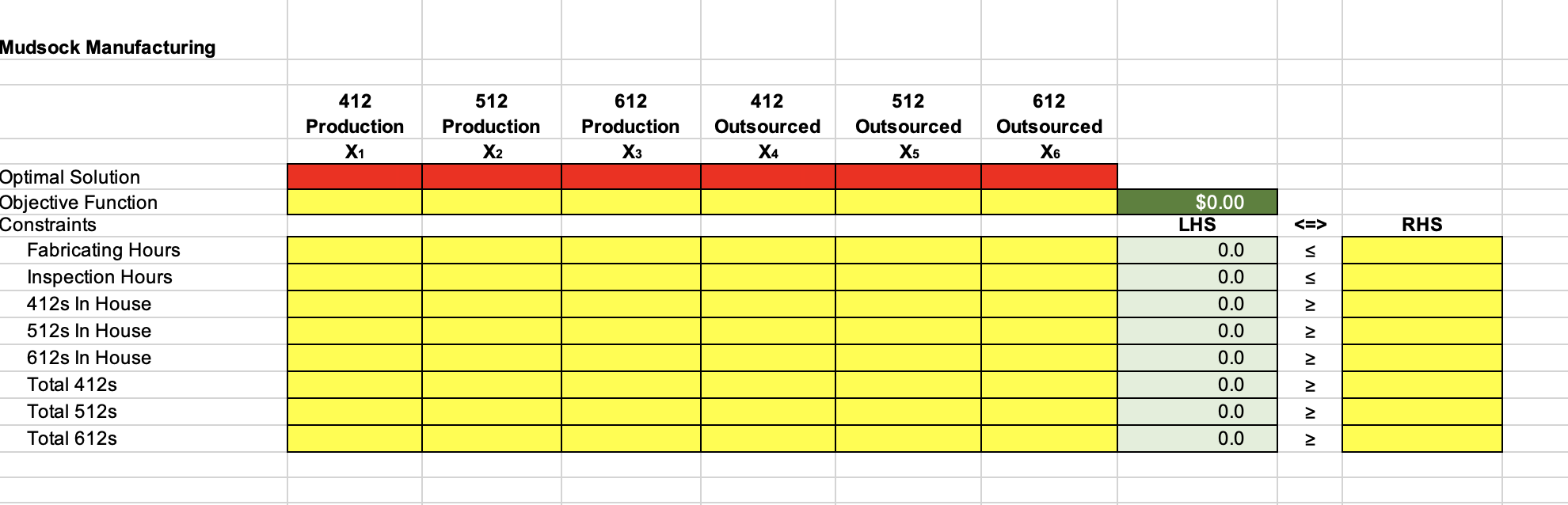
Mudsock Manufacturing produces three types of valves: V412, V512, V612. It has a firm order from Acme Inc. for 2000 V412s, 3750 V512s, and 1700 V612s. Between now and the delivery date Mudsock has 16,500 fabrication hours and 1600 inspection hours, which is not enough to manufacture the total quantity ordered. The time required for each type of valve, cost to manufacture in-house, and cost to outsource are included in the table below. Mudsock wants to manufacture at least 60% of each valve in-house. How many of each type of valve should be manufactured in house and how many outsourced? What will be the total cost of the order? You will open and modify the spreadsheet you developed earlier. You note that the model in MBE2 is a much simpler program, with only 2 decision variable and 4 constraints (plus non-negativity). The production problem has 6 variables and 8 constraints. Is there an easy way to modify your previous solution to solve this more complex problem? The "LHS" column, column D, of your current spreadsheet contains formulas to multiply the coefficients from the Objective Function and each Constraint by the Optimal Solution in row 10 . Using Row 10 as an example, the total printing time consumed is: D10=B10B$5+C10C$5 To modify this for a six-variable system, you will have to make the equation much longer. There will be 6 columns for variables, pushing the LHS column out 4 columns to column H : H10=B10B$5+C10C$5+D10D$5+E10E$5+F10F$5+G10G$5 You quickly realize that if the problem contained several dozen variables that the equation would become very long, very complex, and very easy to make a simple mistake entering all the variables. Fortunately, you find an easy solution an Excel function called SUMPRODUCT. =SUMPRODUCT (First Row in the Equation, Second Row in the Equation) For the original equation, the formula in cell D10 would look like this: = SUMPRODUCT(B5:C5,B10:C10) This formula SUMS the PRODUCT of the two rows in question. The formula reads the equation as: =B5B10+C5C10 You decide to incorporate this formula into your Linear Program, allowing you to easily modify this spreadsheet to solve any size program you must develop. You also note that you can use it to sum the product of two columns, or more than 2 columns or 2 rows. Solution: You will build a linear program in excel, label the marginal cells to properly identify decision variables, the objective function, and constraints, input the coefficients from the problem, install Solver, use Solver to provide your production mix, and derive your expected profit margin. Construct the Model: NOTE: The illustrations will be off 1 row as I changed the MBE2 problem. The cell references in the steps should be correct even though they may disagree with the illustrations. The illustrations are typically off by 1 row. 1. Open your MBE2 solution, "MBA690 MBE3" 2. Insert a new worksheet and label the tab for that worksheet "Production" 3. Enter "Mudsock Manufacturing" in cell A1 4. Insert SUMPRODUCT function in cell D7: =SUMPRODUCT(B\$5:C\$\$,B8:C8) - Be sure to include the "\$" for row 5, anchoring row 5 (your optimal solution) to be used for all Constraint and Objective Function calculations - If you have done it correctly, the value in cell D8 should not change 5. Copy the SUMPRODUCT formula from the previous step to D6, D9, D10, and D11 6. Expand the number of columns to include 6 variables 7. Expand the number of columns to include 6 variables 8. Expand the number of rows to include 8 constraints 9. Add the row labels: 10. Label the columns (Decision Variables) 11. Add the proper equality signs between LHS (actual) and RHS (Available or Required) 1. Solve - Using the instructions from MBE2, finish inputting the spreadsheet and solve - Note that, as stated in class, the lowest cost to produce the order only includes the minimum quantity for each type of valve (2000, 3750, and 1700) - Also note that, as you inserted the columns and rows, solver adjusted as well Mudsock Manufacturing Optimal Solution Objective Function Constraints \begin{tabular}{l|l|} & RHS \\ & \\ & \\ & \\ & \\ & \\ & \\ & \\ & \\ & \\ \end{tabular}