This is my question:

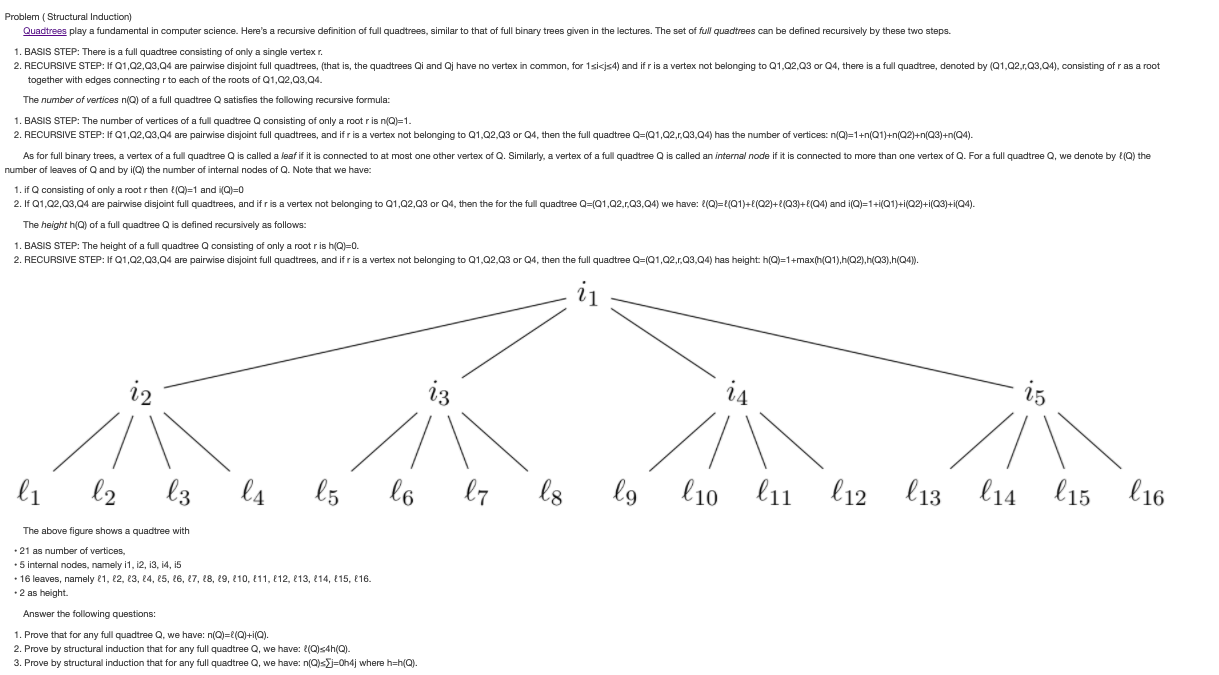
Problem ( Structural Induction) Quadtrees play a fundamental in computer science. Here's a recursive definition of full quadtrees, similar to that of full binary trees given in the lectures. The set of foll quadtrees can be defined recursively by these two steps. 1. BASIS STEP: There is a full quadtree consisting of only a single vertex r. 2. RECURSIVE STEP: If Q1,02,03,Q4 are pairwise disjoint full quadtrees, (that is, the quadtrees Qi and Oj have no vertex in common, for 1sicjs4) and if r is a vertex not belonging to Q1,Q2,Q3 or Q4, there is a full quadtree, denoted by (Q1,Q2,r,Q3,Q4), consisting of r as a root together with edges connecting r to each of the roots of Q1,02,03,Q4. The number of vertices n(Q) of a full quadtree Q satisfies the following recursive formula: 1. BASIS STEP: The number of vertices of a full quadtree Q consisting of only a root r is n(Q)=1. 2. RECURSIVE STEP: If Q1,02,03,Q4 are pairwise disjoint full quadtrees, and if r is a vertex not belonging to Q1,Q2,Q3 or Q4, then the full quadtree Q=(Q1,Q2,r,Q3,Q4) has the number of vertices: n(Q)=1+n(Q1)+n(Q2)+n(Q3)+n(Q4). As for full binary trees, a vertex of a full quadtree @ is called a fear if it is connected to at most one other vertex of Q. Similarly, a vertex of a full quadtree @ is called an internal node if it is connected to more than one vertex of Q. For a full quadtree Q, we denote by {(Q) the number of leaves of Q and by i(Q) the number of internal nodes of Q. Note that we have: 1. if Q consisting of only a root r then {(Q)=1 and i(Q)=0 2. If Q1,02,Q3,Q4 are pairwise disjoint full quadtrees, and if r is a vertex not belonging to Q1,Q2,Q3 or Q4, then the for the full quadtree Q=(Q1,Q2,r,Q3,Q4) we have: ((Q)=(Q1)+[(Q2)+((Q3)+8(Q4) and i(Q)=1+i(Q1)+i(Q2)+i(Q3)+i(Q4). The height h(Q) of a full quadtree Q is defined recursively as follows: 1. BASIS STEP: The height of a full quadtree Q consisting of only a root r is h(Q)=0. 2. RECURSIVE STEP: If Q1,02,Q3,Q4 are pairwise disjoint full quadtrees, and if r is a vertex not belonging to Q1,Q2,Q3 or Q4, then the full quadtree Q=(Q1,Q2,r,Q3,Q4) has height: h(Q)=1+max(h(Q1),h(Q2),h(Q3),h(Q4)). 21 13 25 l10 411 212 413 214 215 The above figure shows a quadtree with . 21 as number of vertices, 5 internal nodes, namely i1, 12, i3, 14, is 16 leaves, namely 21, 82, 83, 24, 85, 16, 17, 18, 19, (10, 11, 212, 213, (14, $15, 816. 2 as height. Answer the following questions: 1. Prove that for any full quadtree Q, we have: n(Q)=8(Q)+i(Q). 2. Prove by structural induction that for any full quadtree Q, we have: ((Q)s4h(Q). 3. Prove by structural induction that for any full quadtree Q, we have: n(Q)s)j=Oh4j where h=h(Q)