Question: This is ONE question. 2. (-/10 Points) DETAILS DEVORESTAT9 S.AE.024 MY NOTES ASK YOUR TEACHER Example 5.23 Consider a simulation experiment in which the population
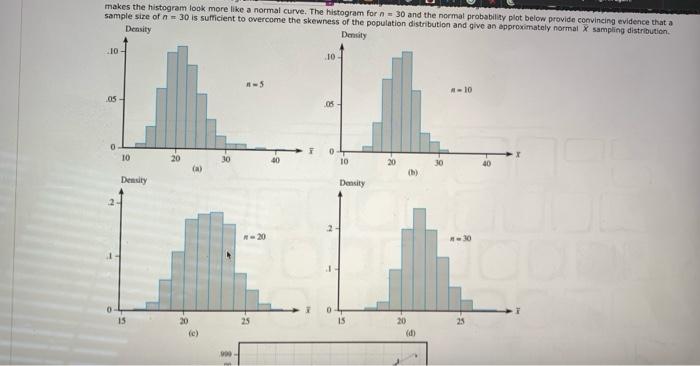
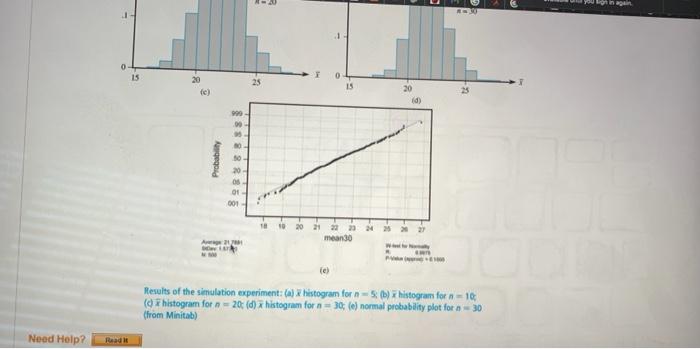
This is ONE question. 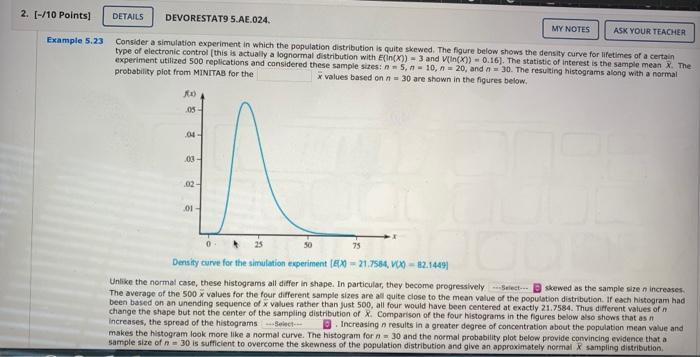

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


