This is only a one problem, please kindly help me answer all the blank. I would really appreciate if you answer all of the blank here. Thank you so much! God bless!

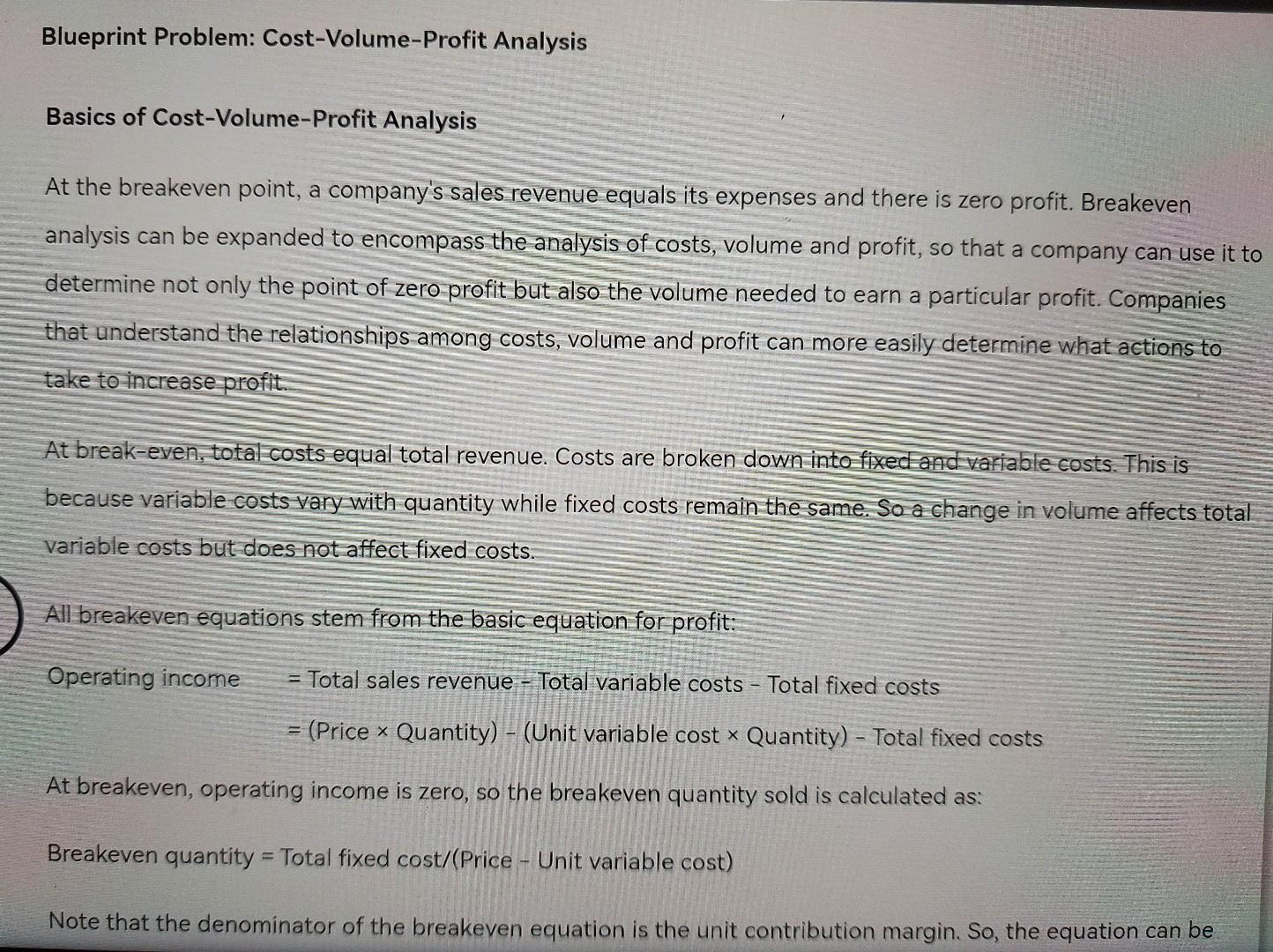
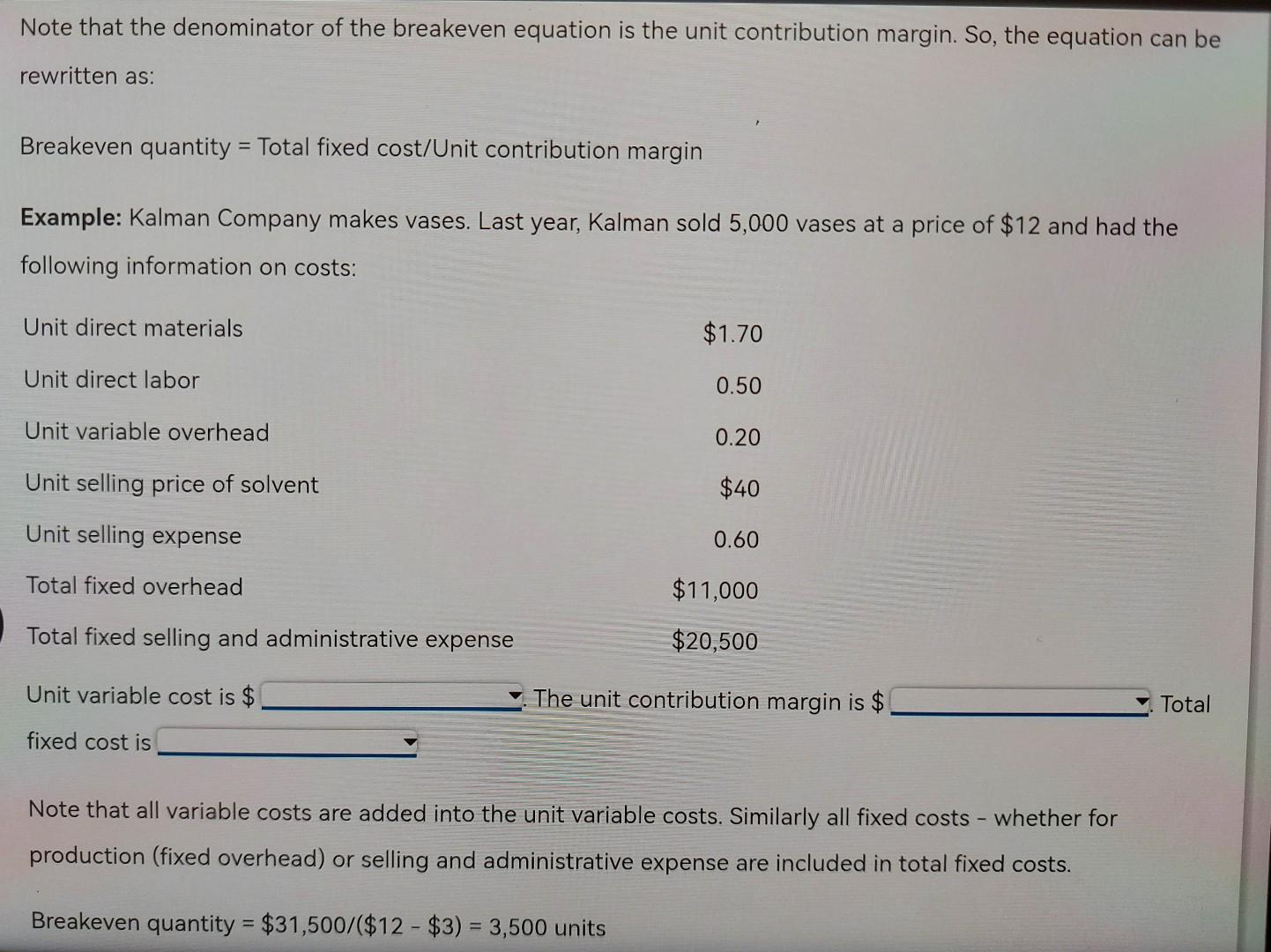
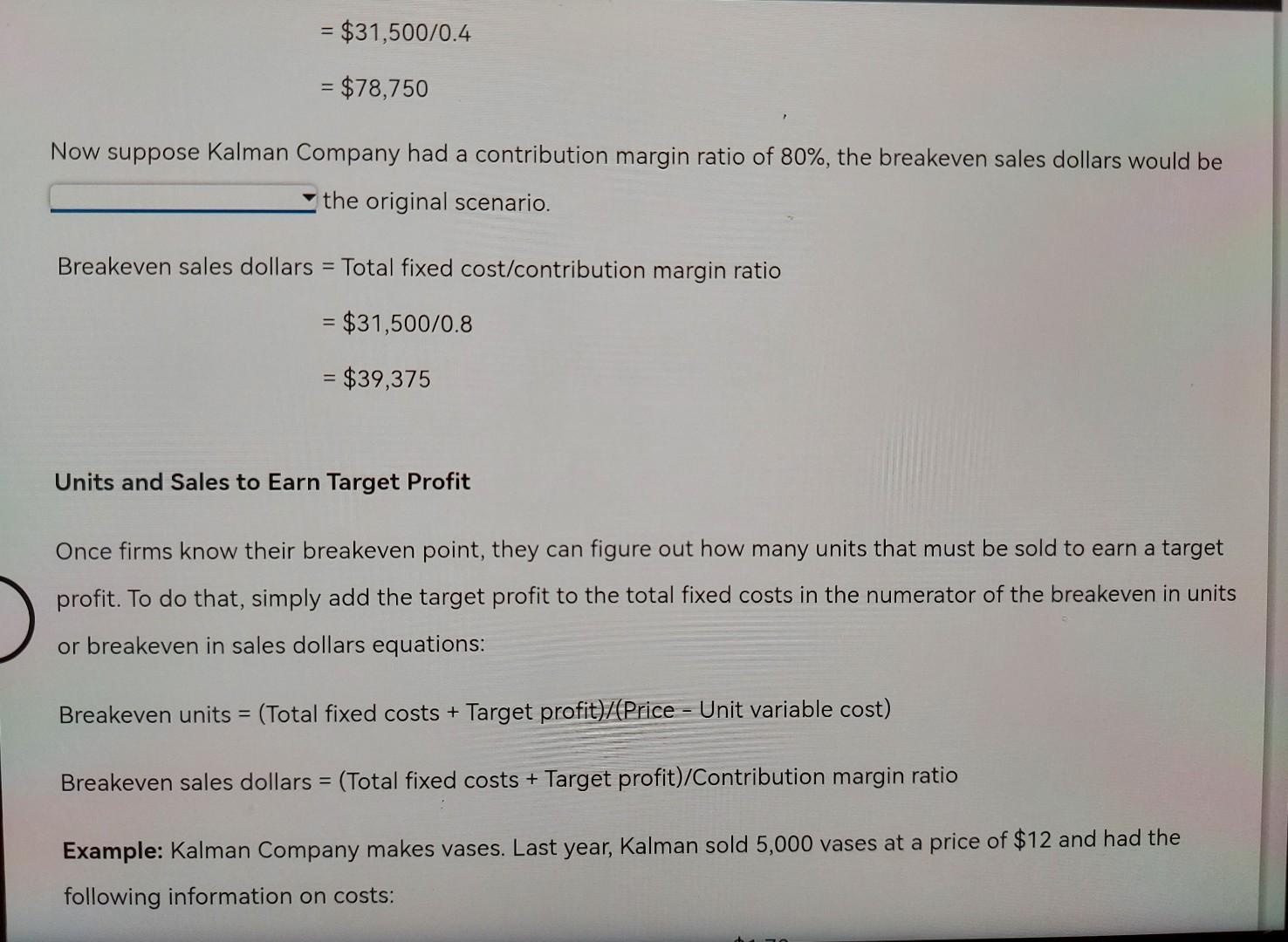
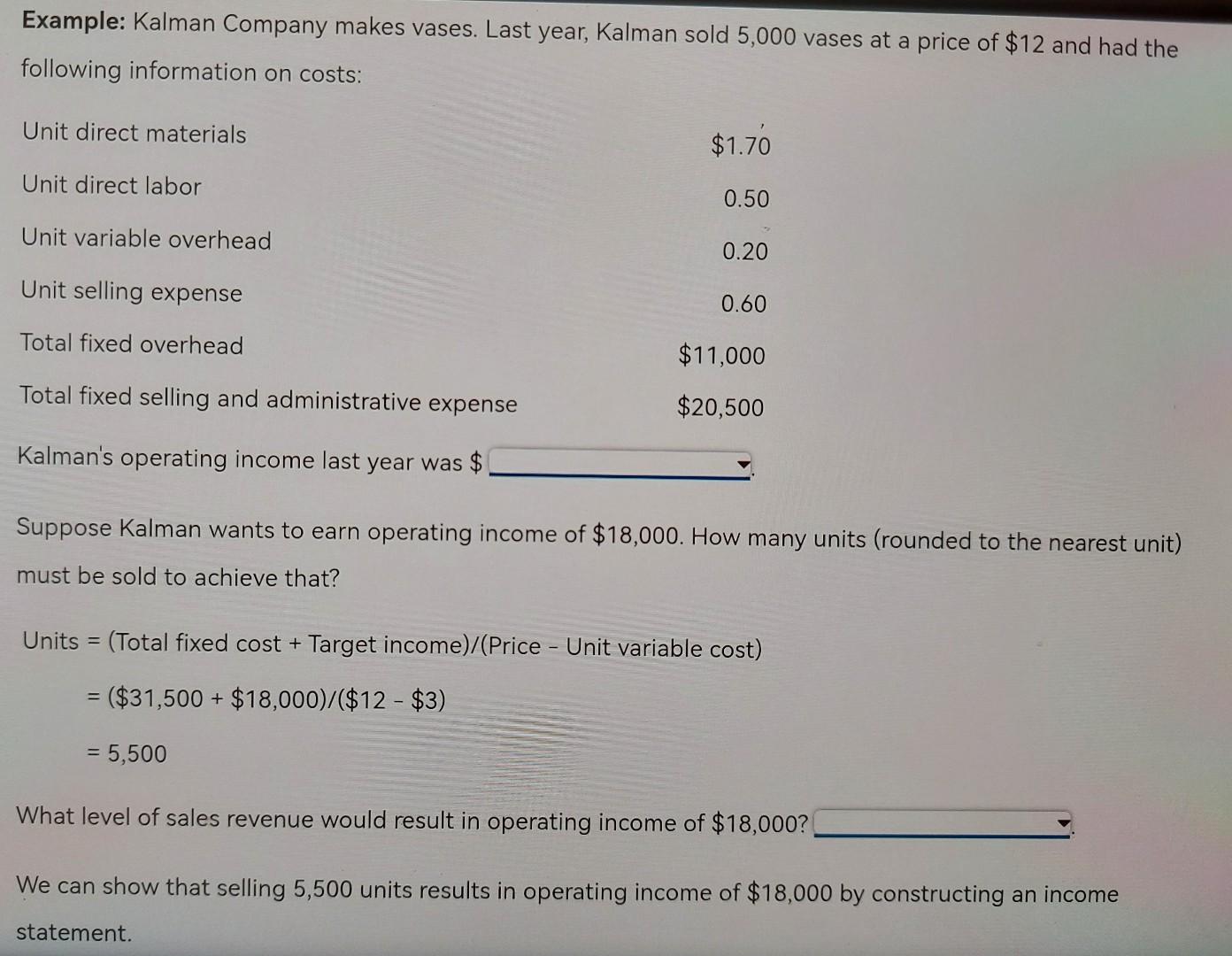
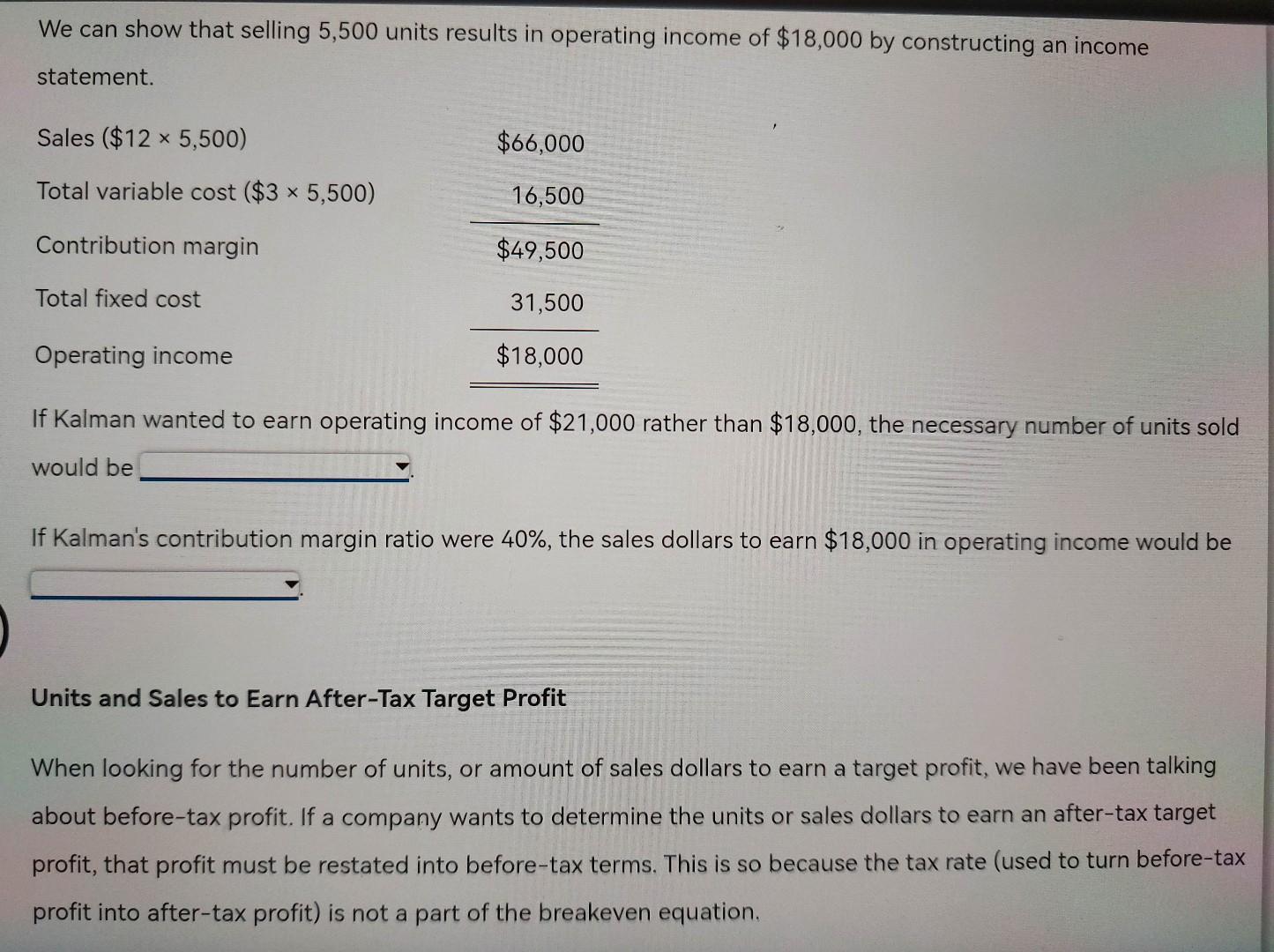
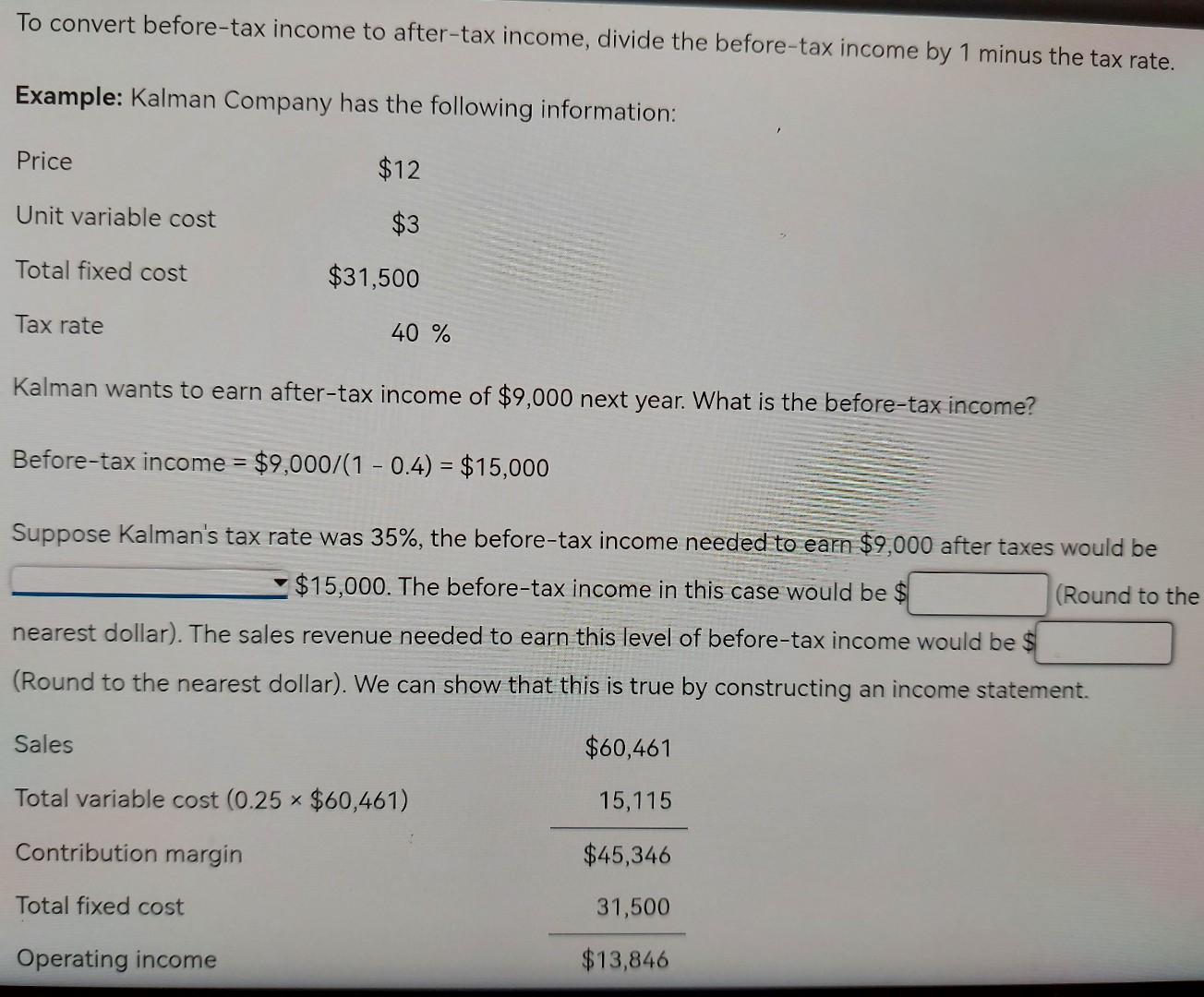
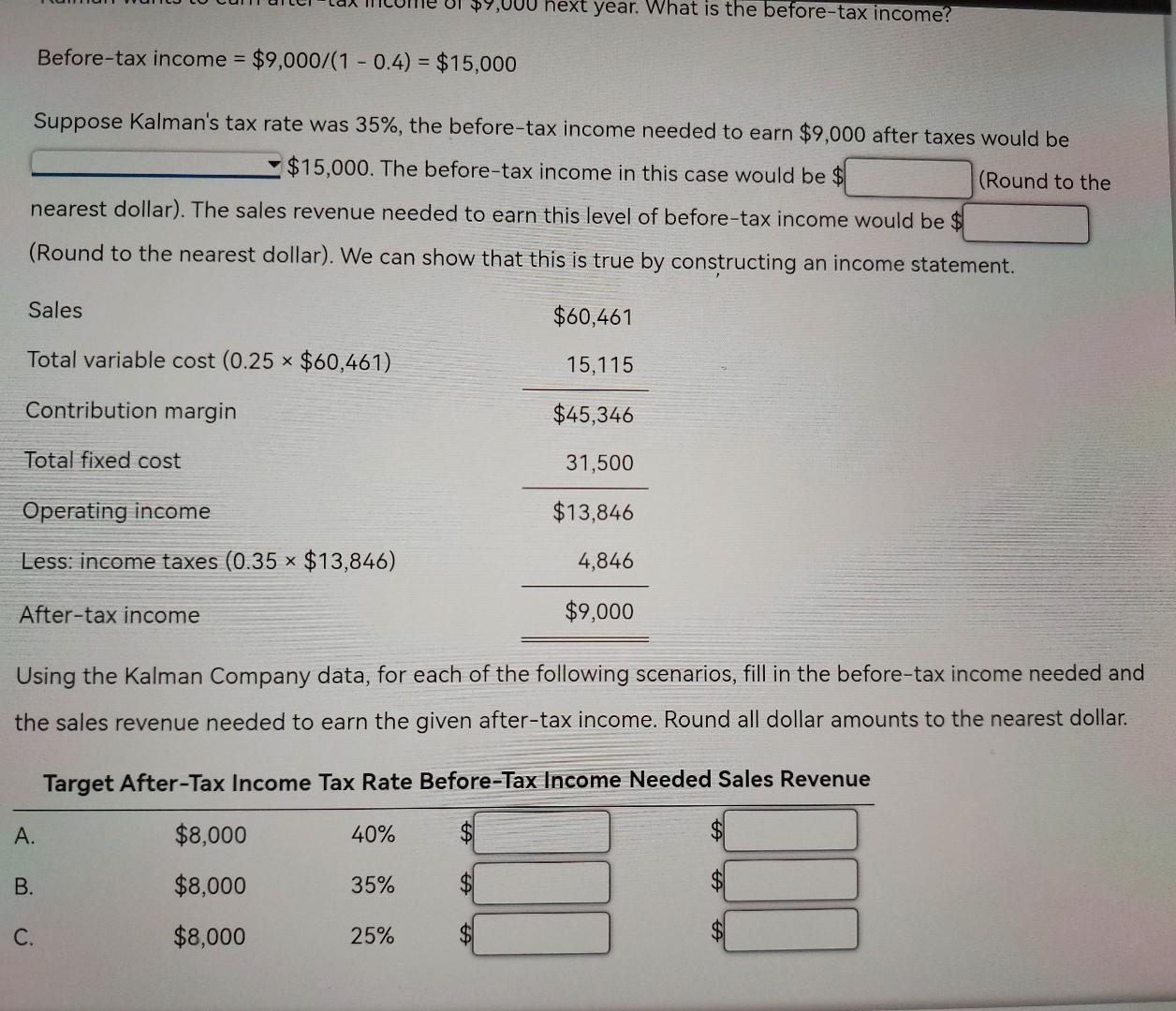
Blueprint Problem: Cost-Volume-Profit Analysis Basics of Cost-Volume-Profit Analysis At the breakeven point, a company's sales revenue equals its expenses and there is zero profit. Breakeven analysis can be expanded to encompass the analysis of costs, volume and profit, so that a company can use it to determine not only the point of zero profit but also the volume needed to earn a particular profit. Companies that understand the relationships among costs, volume and profit can more easily determine what actions to take to increase profit. At break-even, total costs equal total revenue. Costs are broken down into fixed and variable costs. This is because variable costs vary with quantity while fixed costs remain the same. So a change in volume affects total variable costs but does not affect fixed costs. All breakeven equations stem from the basic equation for profit: Operating income = Total sales revenue - Total variable costs - Total fixed costs = (Price x Quantity) - (Unit variable cost * Quantity) - Total fixed costs At breakeven, operating income is zero, so the breakeven quantity sold is calculated as: Breakeven quantity = Total fixed cost/(Price - Unit variable cost) Note that the denominator of the breakeven equation is the unit contribution margin. So, the equation can be Note that the denominator of the breakeven equation is the unit contribution margin. So, the equation can be rewritten as: Breakeven quantity = Total fixed cost/Unit contribution margin Example: Kalman Company makes vases. Last year, Kalman sold 5,000 vases at a price of $12 and had the following information on costs: Unit direct materials $1.70 Unit direct labor 0.50 Unit variable overhead 0.20 Unit selling price of solvent $40 Unit selling expense 0.60 Total fixed overhead $11,000 Total fixed selling and administrative expense $20,500 Unit variable cost is $ The unit contribution margin is $ Total fixed cost is Note that all variable costs are added into the unit variable costs. Similarly all fixed costs - whether for production (fixed overhead) or selling and administrative expense are included in total fixed costs. Breakeven quantity = $31,500/($12 - $3) = 3,500 units Breakeven quantity = $31,500/($12 - $3) = 3,500 units We can show that selling 3,500 units does result in breaking even by constructing an income statement. Sales ($12 ~ 3,500) $42,000 Total variable cost ($3 x 3,500) 10,500 Contribution margin $31,500 Total fixed cost 31,500 Operating income $0 Breakeven sales revenue is found by multiplying the breakeven quantity by price. Alternatively, one can multiply both sides of the breakeven equation by price so that the equation for breakeven sales revenue is: Breakeven sales = Total fixed cost/Contribution margin ratio Select "Yes or No" from the following ratios that can be computed by contribution margin: Select "Yes or No" from the following ratios that can be computed by contribution margin: Price - unit variable cost Unit contribution margin/Price Total contribution margin/Price Total contribution margin/Sales (Price - unit variable cost)/Price (Price - unit variable cost)/Sales Price/(Price - unit variable cost) (1 - variable cost ratio)/Price Price/Unit contribution margin (1 - variable cost ratio) Example: Kalman Company makes vases. Last year, Kalman sold 5,000 vases at a price of $12 and had unit variable cost of $3. Total fixed costs were $37,800. The contribution margin ratio was Breakeven sales were $ Suppose Kalman Company had a contribution margin ratio of 40%, the breakeven sales dollars would be the original scenario. Breakeven sales dollars = Total fixed cost/contribution margin ratio = $31,500/0.4 = $78,750 Now suppose Kalman Company had a contribution margin ratio of 80%, the breakeven sales dollars would be the original scenario. Breakeven sales dollars = Total fixed cost/contribution margin ratio = $31,500/0.8 = $39,375 Units and Sales to Earn Target Profit Once firms know their breakeven point, they can figure out how many units that must be sold to earn a target profit. To do that, simply add the target profit to the total fixed costs in the numerator of the breakeven in units or breakeven in sales dollars equations: Breakeven units = (Total fixed costs + Target profit)/(Price - Unit variable cost) Breakeven sales dollars = (Total fixed costs + Target profit)/Contribution margin ratio Example: Kalman Company makes vases. Last year, Kalman sold 5,000 vases at a price of $12 and had the following information on costs: Example: Kalman Company makes vases. Last year, Kalman sold 5,000 vases at a price of $12 and had the following information on costs: Unit direct materials $1.76 Unit direct labor 0.50 Unit variable overhead 0.20 Unit selling expense 0.60 Total fixed overhead $11,000 Total fixed selling and administrative expense $20,500 Kalman's operating income last year was $ Suppose Kalman wants to earn operating income of $18,000. How many units (rounded to the nearest unit) must be sold to achieve that? Units = (Total fixed cost + Target income)/(Price - Unit variable cost) = = ($31,500 + $18,000)/($12 - $3) = 5,500 What level of sales revenue would result in operating income of $18,000? We can show that selling 5,500 units results in operating income of $18,000 by constructing an income statement. We can show that selling 5,500 units results in operating income of $18,000 by constructing an income statement. Sales ($12 x 5,500) $66,000 Total variable cost ($3 x 5,500) 16,500 Contribution margin $49,500 Total fixed cost 31,500 Operating income $18,000 If Kalman wanted to earn operating income of $21,000 rather than $18,000, the necessary number of units sold would be If Kalman's contribution margin ratio were 40%, the sales dollars to earn $18,000 in operating income would be Units and Sales to Earn After-Tax Target Profit When looking for the number of units, or amount of sales dollars to earn a target profit, we have been talking about before-tax profit. If a company wants to determine the units or sales dollars to earn an after-tax target profit, that profit must be restated into before-tax terms. This is so because the tax rate (used to turn before-tax profit into after-tax profit) is not a part of the breakeven equation. To convert before-tax income to after-tax income, divide the before-tax income by 1 minus the tax rate. Example: Kalman Company has the following information: Price $12 Unit variable cost $3 Total fixed cost $31,500 Tax rate 40 % Kalman wants to earn after-tax income of $9,000 next year. What is the before-tax income? Before-tax income = $9,000/(1 - 0.4) = $15,000 Suppose Kalman's tax rate was 35%, the before-tax income needed to earn $9,000 after taxes would be $15,000. The before-tax income in this case would be $ (Round to the nearest dollar). The sales revenue needed to earn this level of before-tax income would be $ (Round to the nearest dollar). We can show that this is true by constructing an income statement. Sales $60,461 Total variable cost (0.25 * $60,461) 15,115 Contribution margin $45,346 Total fixed cost 31,500 Operating income $13,846 UI $9,000 hext year. What is the before-tax income? Before-tax income = $9,000/(1 - 0.4) = $15,000 = Suppose Kalman's tax rate was 35%, the before-tax income needed to earn $9,000 after taxes would be $15,000. The before-tax income in this case would be $ (Round to the nearest dollar). The sales revenue needed to earn this level of before-tax income would be $ (Round to the nearest dollar). We can show that this is true by constructing an income statement. Sales $60,461 Total variable cost (0.25 $60,461) 15,115 Contribution margin $45,346 Total fixed cost 31,500 Operating income $13,846 Less: income taxes (0.35 x $13,846) 4,846 After-tax income $9,000 Using the Kalman Company data, for each of the following scenarios, fill in the before-tax income needed and the sales revenue needed to earn the given after-tax income. Round all dollar amounts to the nearest dollar. Target After-Tax Income Tax Rate Before-Tax Income Needed Sales Revenue A. $8,000 40% B. $8,000 35% C. $8,000 25% $