this is the example.

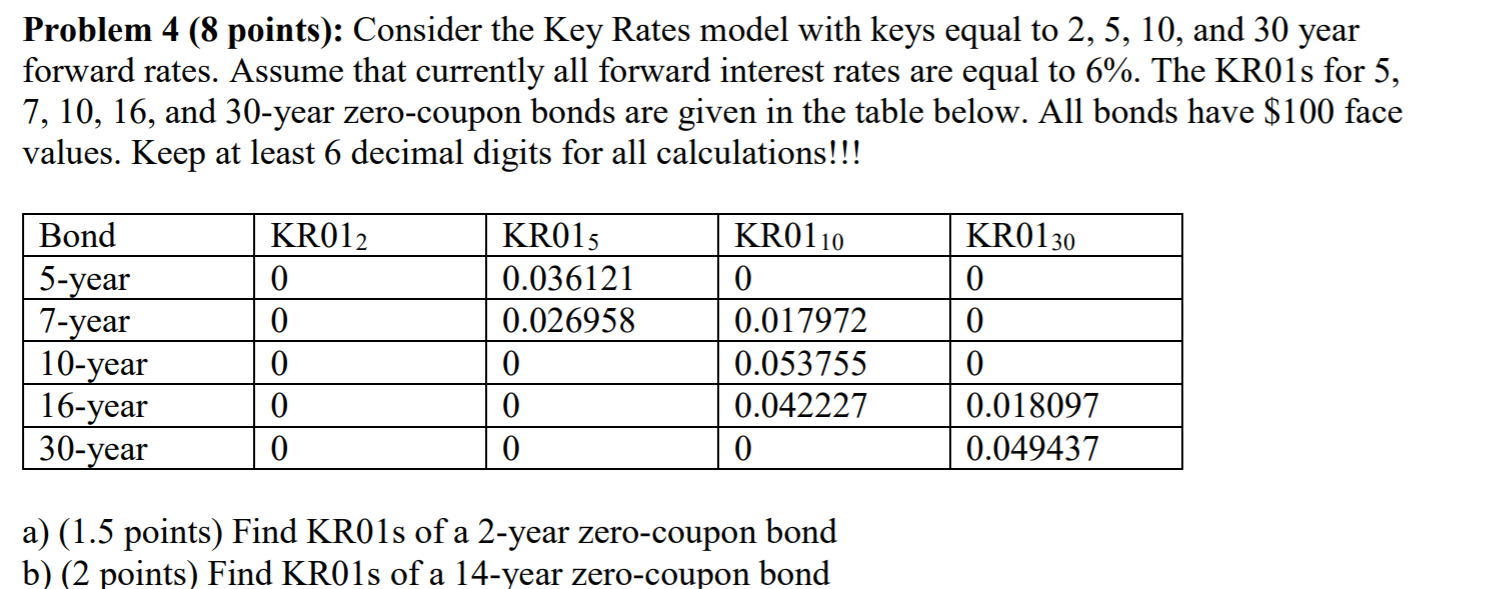
0 0 0 0 0 0 Problem 3 (7 points): Assume that you have ten 11-year 4% coupon par bonds and you want to hedge this portfolio using securities S1, S2, S3 and 54. The key rate 01s of these securities are given below. How many securities do you need to buy/sell? Security 2-year key 5-year key 10-year key 30-year key S1 0.01 S2 0.01 S3 0.02 0.06 0.645 0 S3 0 0.11 Solution: We need to find key rate 01s for your portfolio. YTM11 depends only on YTM10 and YTM30 t2-t 1% increase in YTM10 leads to =0.95% increase in YTMU1 ta-t1 1% increase in YTM2. leads to =0.05% increase in YTM11 ta-t1 30-10 So, for every 11-year bond in your portfolio: 0 0 30-11 . 30-10 11-10 t-ti = dP dP dy11 C 1 11 1- 100 - dyt dy11 dyt yi 1+ 11 + Since your 11-year bonds are par bonds then 911 = coupon rate c = 4%, C = cxF = 0.04x100 0.04 x 100. Thus, 100 - = 100 O and 1 x))+co dy11 dyt Yn * (1 +24) Y11 0.04 dy11 - 4 (-6) (-0.6(1-(102) '] * 0.042 dy11 - H 0.042 1.0222)] dP dP dy11 dy11 1- X dyt dy11 dyt y11 dyt dyt 4 dy11 (1 X 15-882.902x dyt dyt -882.902 x dy11 = -882.902 x 0.95 = -838.757 for t = 10 dyt dy11 -882.902 x -= -882.902 x 0.05 = -44.1451 for t = 30 dyt 838.757 44.1451 Thus KR0110 = =0.0838757 and KRO130 =0.00441451 for every bond in 10,000 your portfolio. Since you have 100 bonds: 2-year 5-year 10-year 30-year 0 0 8.38757 0.441451 Now we need to solve the system of equations: N4 x 0.01 + N2 x 0 + N2 x 0.02 + N4 x 0 = 0 (1) N, XO + N2 x 0.01 +N3 x 0.06 + N4 x 0 = 0 (2 N, X0+ N2 x 0+N3 x 0.645+N4 x 0 = -8.38757 (3 W, x 0 + N2 x 0 +N3 x 0 + N4 * 0.11 = -0.441451 (4) 10,000 From (4) we get N4 = -4, from (3) we get N3 = -13 from (2) we get N2 = -78, and from (1) we get Ni = -26: Answer: sell 26 of S1, 78 of S2, 13 of S3 and 4 of 54. Problem 4 (8 points): Consider the Key Rates model with keys equal to 2, 5, 10, and 30 year forward rates. Assume that currently all forward interest rates are equal to 6%. The KR0ls for 5, 7, 10, 16, and 30-year zero-coupon bonds are given in the table below. All bonds have $100 face values. Keep at least 6 decimal digits for all calculations!!! KR0130 Bond 5-year 7-year 10-year 16-year 30-year KR012 0 0 0 0 0 KR015 0.036121 0.026958 0 0 0 KR0110 0 0.017972 0.053755 0.042227 0 0 0 0 0.018097 0.049437 a) (1.5 points) Find KR0ls of a 2-year zero-coupon bond b) (2 points) Find KRO1s of a 14-year zero-coupon bond 0 0 0 0 0 0 Problem 3 (7 points): Assume that you have ten 11-year 4% coupon par bonds and you want to hedge this portfolio using securities S1, S2, S3 and 54. The key rate 01s of these securities are given below. How many securities do you need to buy/sell? Security 2-year key 5-year key 10-year key 30-year key S1 0.01 S2 0.01 S3 0.02 0.06 0.645 0 S3 0 0.11 Solution: We need to find key rate 01s for your portfolio. YTM11 depends only on YTM10 and YTM30 t2-t 1% increase in YTM10 leads to =0.95% increase in YTMU1 ta-t1 1% increase in YTM2. leads to =0.05% increase in YTM11 ta-t1 30-10 So, for every 11-year bond in your portfolio: 0 0 30-11 . 30-10 11-10 t-ti = dP dP dy11 C 1 11 1- 100 - dyt dy11 dyt yi 1+ 11 + Since your 11-year bonds are par bonds then 911 = coupon rate c = 4%, C = cxF = 0.04x100 0.04 x 100. Thus, 100 - = 100 O and 1 x))+co dy11 dyt Yn * (1 +24) Y11 0.04 dy11 - 4 (-6) (-0.6(1-(102) '] * 0.042 dy11 - H 0.042 1.0222)] dP dP dy11 dy11 1- X dyt dy11 dyt y11 dyt dyt 4 dy11 (1 X 15-882.902x dyt dyt -882.902 x dy11 = -882.902 x 0.95 = -838.757 for t = 10 dyt dy11 -882.902 x -= -882.902 x 0.05 = -44.1451 for t = 30 dyt 838.757 44.1451 Thus KR0110 = =0.0838757 and KRO130 =0.00441451 for every bond in 10,000 your portfolio. Since you have 100 bonds: 2-year 5-year 10-year 30-year 0 0 8.38757 0.441451 Now we need to solve the system of equations: N4 x 0.01 + N2 x 0 + N2 x 0.02 + N4 x 0 = 0 (1) N, XO + N2 x 0.01 +N3 x 0.06 + N4 x 0 = 0 (2 N, X0+ N2 x 0+N3 x 0.645+N4 x 0 = -8.38757 (3 W, x 0 + N2 x 0 +N3 x 0 + N4 * 0.11 = -0.441451 (4) 10,000 From (4) we get N4 = -4, from (3) we get N3 = -13 from (2) we get N2 = -78, and from (1) we get Ni = -26: Answer: sell 26 of S1, 78 of S2, 13 of S3 and 4 of 54. Problem 4 (8 points): Consider the Key Rates model with keys equal to 2, 5, 10, and 30 year forward rates. Assume that currently all forward interest rates are equal to 6%. The KR0ls for 5, 7, 10, 16, and 30-year zero-coupon bonds are given in the table below. All bonds have $100 face values. Keep at least 6 decimal digits for all calculations!!! KR0130 Bond 5-year 7-year 10-year 16-year 30-year KR012 0 0 0 0 0 KR015 0.036121 0.026958 0 0 0 KR0110 0 0.017972 0.053755 0.042227 0 0 0 0 0.018097 0.049437 a) (1.5 points) Find KR0ls of a 2-year zero-coupon bond b) (2 points) Find KRO1s of a 14-year zero-coupon bond