THIS IS THE LINK https://phet.colorado.edu/sims/html/masses-and-springs-basics/latest/masses-and-springs-basics_en.html , PLEASE DO THIS ACTIVITY ON A COMPUTER GO TO THE WEBSITE LINK THAT I PUT THE SAME LINK UNDER MATERIALS PLEASE COPY THE LINK ON YOUR COMPUTER TO DO THE EXCERSICES, THANK YOU.

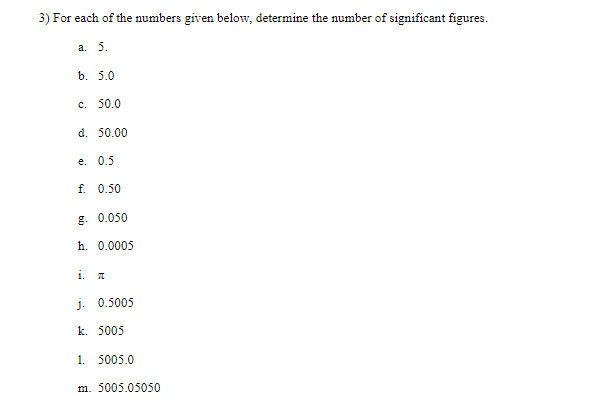
Objective: In this lab exercise we will be discussing measurement accuracy and precision, significant figures, and scientific notation. The notion of measurement accuracy and precision is essential to properly communicating results of a measurement and the final uncertainty in a measurement can be no better than the measurement with the lowest level of accuracy. For example, if you know you are traveling, in a car, at exactly 65 miles per hour for exactly 1 hour. Then you know you traveled exactly 65 miles. However, there is actually uncertainty in the measurement. In practice if you claim you are traveling 65 miles per hour as read on a speedometer with 1 mile per hour resolution then convention states you are traveling 65 1 1 mph. Similarly, if your watch has resolution of only 1 second then you know your travel time is 1 hr 1 1 sec which we can rewrite as 1 0.0003 hrs. This would be the most accurate way to express the uncertainty. But we might just choose to write out that we traveled for 1.000 hrs where we chose to round to 4 significant figures. It should be clear in this case the more significant uncertainty in the determination of how far you actually drove in the hour is the speed at which you are traveling. Therefore, one can not claim a distance traveled better than the uncertainty in the speed. That is to say when you multiply (65 mph x 1.000 hrs = 65 miles) you can't claim you drove 65.000 miles since the uncertainty is dominated by the resolution of the speedometer. In this lab exercise we will first complete a worksheet involving measuring the length of an object using the rulers supplied in this handout. We will then perform an exercise involving accuracy versus precision, followed by a few exercises related to expressing numbers using scientific notation and performing relatively simple calculations concentrating on making sure to express the final answer with the correct significant figures. Finally, you will be running a simulation to determine the spring constant of a spring using several different methods. The formulas to determine the spring constant are given to you in this handout. Your job will be to perform the measurements and also determine which method leads to the most accurate result and why.Materials: This handout, printed . A pencil or pen with length -15 cm (6 inches). Don't worry about being very close to this length, a common pencil or pen is between 14 and 16 cm. Attendance or viewing mini-lecture on significant figures and scientific notation. Computer and Internet access to use the following simulation: https://phet.colorado.edu/sims/html/masses-and-springs-basics/latest/masses-and-springs- basics en.html Investigation A: Resolution of a Ruler Purpose: To understand that the resolution of a measurement device determines how precise of a measurement you can make.Reported measurements must always be rounded to the proper number of significant figures. The number of significant figures reported tells you something about how precise the measurement was. As a first step, we'll learn how to look at a number (in a lab report or in a data table, for instance) and determine the number of significant figures. The rules for counting the number of significant figures in quantity are as follows: I. All exact numbers have an infinite number of significant figures. For example, if you count that there are 35 people in the room, then treat the number 35 as a quantity known to infinite number of significant figures. II. If there is a decimal point in the number, don't count the leading zeros, but count all other digits as significant. For example: 0.00120 has three significant figures. The reason for this is that the leading zeros in a number with a decimal point don't tell you anything about the precision of the measurement, just the overall size. III. If there is no decimal point, don't count trailing zeros, but count all other digits as significant. For example: 12300 has three significant figures. The reason for this is that the trailing zeros in a number without a decimal point don't tell you anything about the precision of the measurement, just the overall size.3) For each of the numbers given below, determine the number of significant figures. a. 5. b. 5.0 c. 50.0 d. 50.00 e. 0.5 f. 0.50 g. 0.050 h. 0.0005 1. A j. 0.5005 k. 5005 1. 5005.0 m. 5005.05050Dealing with significant figures in a number with no decimal point can sometimes be confusing. For instance, what if you want to express the number 1000 to 2 sig figs? Expressing a number in scientific notation makes the number of significant figures unambiguous. The number one thousand can be expressed to 2 sig figs using scientific notation: 1.0x10. It can also be expressed to three sig figs: 1.00x10#. Written in scientific notation, a number has a coefficient and an exponent. The coefficient is a number between 1 and 10. The exponent is a whole-number power of 10. The number of significant figures is just the number of significant figures in the coefficient. Another example: 0.00134 in scientific notation is 1.34x10- (the coefficient 1.34 has 3 sig figs). 4) Write the following numbers in scientific notation, using the proper number of significant figures. a) 245,000 b) 0.0045 c) 75 d) 0.33 5) When you report a measurement, the number of decimal places you should record depends on how precise your measurement device is. For example, a meter stick has fine tick marks that are spaced out by one millimeter. Therefore, round to the nearest millimeter when using a meter stick. $5.0 cm would be an appropriate way to report a measurement taken with a meter stick with millimeter tick marks, but 55.0000 cm would not.Note: When using a measurement device the finest "tick" mark is referred to as the least count. For example, a meter stick with millimeter tick marks would have a least count of 0.001 meters. Likewise a stop watch that reports the elapsed time to hundredths of a second would have a least count of 0.01 seconds. For each of the measurements you made of the pencil above, record the measurement below and indicate the number of significant figures you would feel confident in stating. O 10 20 measurement: number of sig figs