This lab uses the Photoelectric Effect Simulator on the PhET website.

PHY202L Name ____________________________________ Lab 8 - The Photoelectric Effect

Introduction

The Photoelectric effect is a phenomenon in which electrically charged particles are released from or within a material when it absorbselectromagnetic radiation. The effect is often defined as the ejection ofelectronsfrom ametal plate when light falls on it. In fact, theradiant energy may beinfrared, visible, orultravioletlight,X-rays, orgamma rays; the material may be a solid, liquid, or gas, and the released particles may beions(electrically charged atoms or molecules) as well as electrons. The phenomenon was seminally significant in the development of modern physics because of the questions it raised about the nature of light?particle versus wavelike behavior?that were finally resolved byAlbert Einsteinin 1905.

Einstein formulated a new corpuscular theory of light in which each particle of light, orphoton, contains a fixed amount of energy, orquantum, that depends on the light's frequency. A photon carries an energy given by E = hf

wherefis the frequency of the light andhis the universal constant that the physicistMax Planckderived in 1900 to explain the wavelength distribution ofblackbodyradiation (electromagnetic radiation emitted from a hot object). The constant is known as Planck's constant and has the value:

h = 6.626 10^?34Joule Second

Einstein assumed that a photon would penetrate the material and transfer its energy to an electron. As the electron moved through the metal at high speed and finally escapes from the material, its kinetic energy is diminished by an amount ? called thework function which represents the energy required for the electron to escape.

By conservation of energy, this reasoning led Einstein to the photoelectric equation: E_k=hf- ? whereE_kis the maximum kinetic energy of the ejected electron. Since the work function's value is a constant for a given material, there is a linear relationship between the incident light frequency and electron kinetic energy. In addition, there is an incident light frequency at which photons transfer just enough energy to enable ejection of an electron from the surface (E_k just exceeds zero); that frequency is called the threshold frequency, and in some publications appears with the symbol f_t .

Sidebar: Start the Photoelectric Effect simulation on the PhET site. This simulation allows you to "see" photons bombarding one of two metal plates in a vacuum chamber, as well as the electrons ejecting from the plate. The plates are connected in series to a voltage source and ammeter. This will be our photoelectric apparatus. The maximum kinetic energy can be measured indirectly with a Photoelectric apparatus by using what is called the stopping voltage. When a voltage is applied across the electrodes, electrons escaping the material find themselves moving through an electric field that wants to stop them before completing their journey to the other electrode. If the field is too great, they turn around and go back to the material's surface. If the field is too low, then all the electrons go to the other electrode; that creates a current in the circuit. At just the right amount of voltage, only the electrons with the greatest kinetic energy reach the other electrode.

(It is the same idea as a ball thrown upward with the greatest KE will go the farthest against the gravity field.)

Since the work done on an electron equals qV, the charge of an electron times the stopping voltage is the kinetic energy of the escaped electron.

Objectives:

1. To understand the importance of Einstein's interpretation of this famous experiment.

2. To understand how this experiment provided evidence for the "particle-like" nature of light.

3. Correctly analyze and interpret graphs of data generated by a simulation of a Photoelectric apparatus.

References:

• Cutnell and Johnson, Physics 10e - Chapter 29.1-2

Procedure:

1. Take a few minutes to acquaint yourself with the simulation controls and data graphs available. Two suggestions:

• You can use the sliders or manually enter values to change the voltage, light intensity, and wavelength. Manually entering values gives you better control, but after changing a number in an input field you must hit the Enter (carriage return) key on your keyboard for the change to take effect.
• Under Options, turn on "show photons".

2. Set the light intensity to 100% and the stopping voltage to zero. Determine the threshold frequencies for Sodium and Platinum. You can use the slider to find a narrow range and then the input field to determine the exact value. You need to wait a few seconds to see whether an electron is released or not when you are close (and yes, it could remind you of turtles at a starting line). Show how you calculated f_tfor one of the materials in the space below.

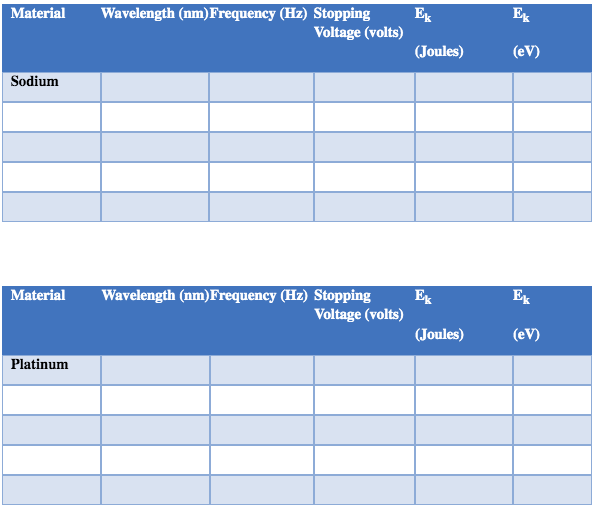
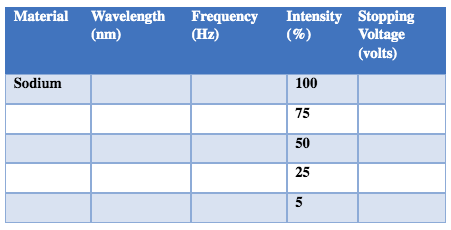
Material Wavelength (nm)Threshold frequency (Hz) Sodium PlatinumMaterial Wavelength (nm) Frequency (Hz) Stopping Ek Voltage (volts) (Joules) (e V) Sodium Material Wavelength (nm)Frequency (Hz) Stopping Ek Ek Voltage (volts) (Joules) (eV) PlatinumMaterial Wavelength Frequency Intensity Stopping (mm) (HZ) (%) Voltage (volts) Sodium 100 75 50 25 5