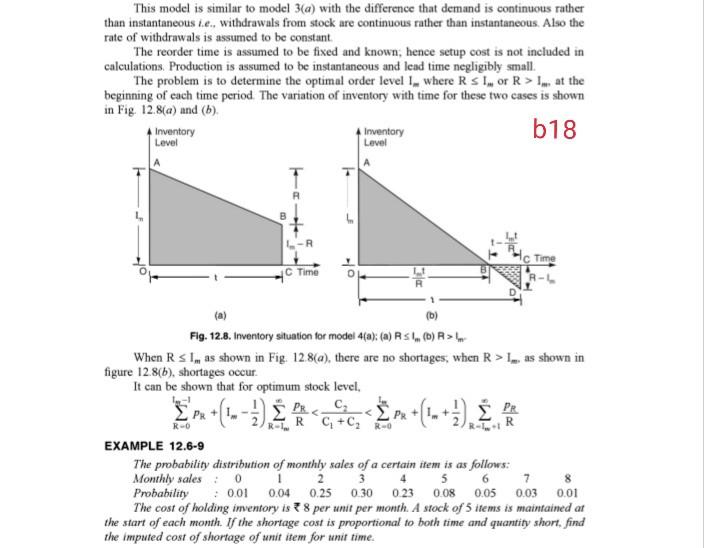
This model is similar to model 3(a) with the difference that demand is continuous rather than instantaneous i.e., withdrawals from stock are continuous rather than instantaneous. Also the rate of withdrawals is assumed to be constant The reorder time is assumed to be fixed and known, hence setup cost is not included in calculations Production is assumed to be instantaneous and lead time negligibly small. The problem is to determine the optimal order level 1. where RSL or R>1. at the beginning of each time period. The variation of inventory with time for these two cases is shown in Fig. 12.8(a) and (b) Inventory Inventory b18 Level Level L-R Time C Time DIE (b) Fig. 12.8. Inventory situation for model 4(a): (a) RS (O)R>L When Rs 1, as shown in Fig. 128(a), there are no shortages, when R>1, as shown in figure 12.8(b), shortages occur. It can be shown that for optimum stock level, PR R-O R-1 RC+C EXAMPLE 12.6-9 The probability distribution of monthly sales of a certain item is as follows: Monthly sales: 0 1 2 3 4 5 6 8 Probability : 0.01 0.04 0.250.30 023 0.08 0.05 0.03 0.01 The cost of holding inventory is 8 per unit per month. A stock of 5 items is maintained at the start of each month. If the shortage cost is proportional to both time and quantity short, find the imputed cost of shortage of unit item for unit time. 7