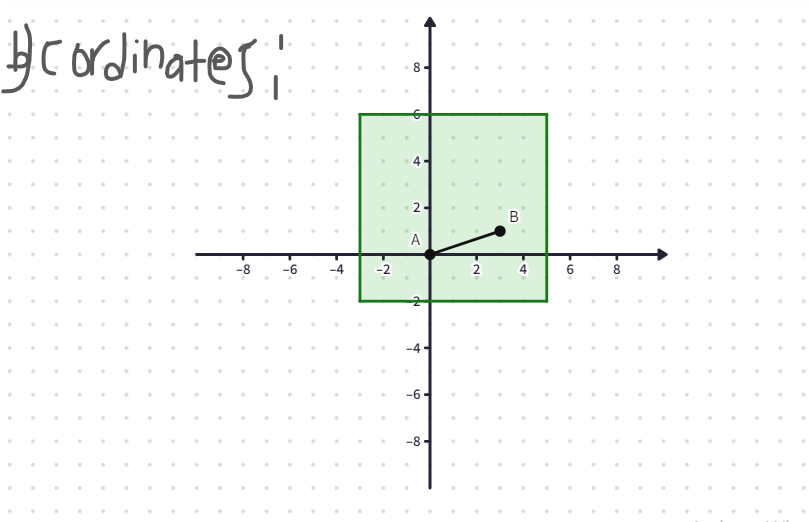
This problem is about the geoboards a. There are nine different locations for the point C to form an isosceles triangle ABC, but they aren't all different triangles. Using transformations, prove that the triangle formed by putting C_1 two pegs up from A and the triangle formed by putting C_2 two pegs down from B are congruent. (The technical term for "peg" is "lattice point." Lattices are of primary importance in number theory; for example, Fermat's last theorem. They also come up everywhere in crystallography and quantum physics.) b. Prove that, if you can go outside the green area, there are infinitely many different pegs at which you can place C to form an isosceles triangle. (Hint: use coordinates to describe them.) Justify why you know that your triangles are isosceles.\f