$[$This problem is designed to give a concrete example of a graph with $n$ vertices such that the number

of paths grows faster than any polynomial in terms of $n.$ This is important later when we start looking

for paths with specific properties $($shortest paths, paths of even or odd length, paths that avoid certain

vertices, etc.$)$ Some of you will be tempted to say "Search all paths...." but this may require a runtime

that grows exponentially or faster. It is important to note that DFS$,$ BFS$,...$ do not search all paths

since these algorithms are polynomial time.$]$

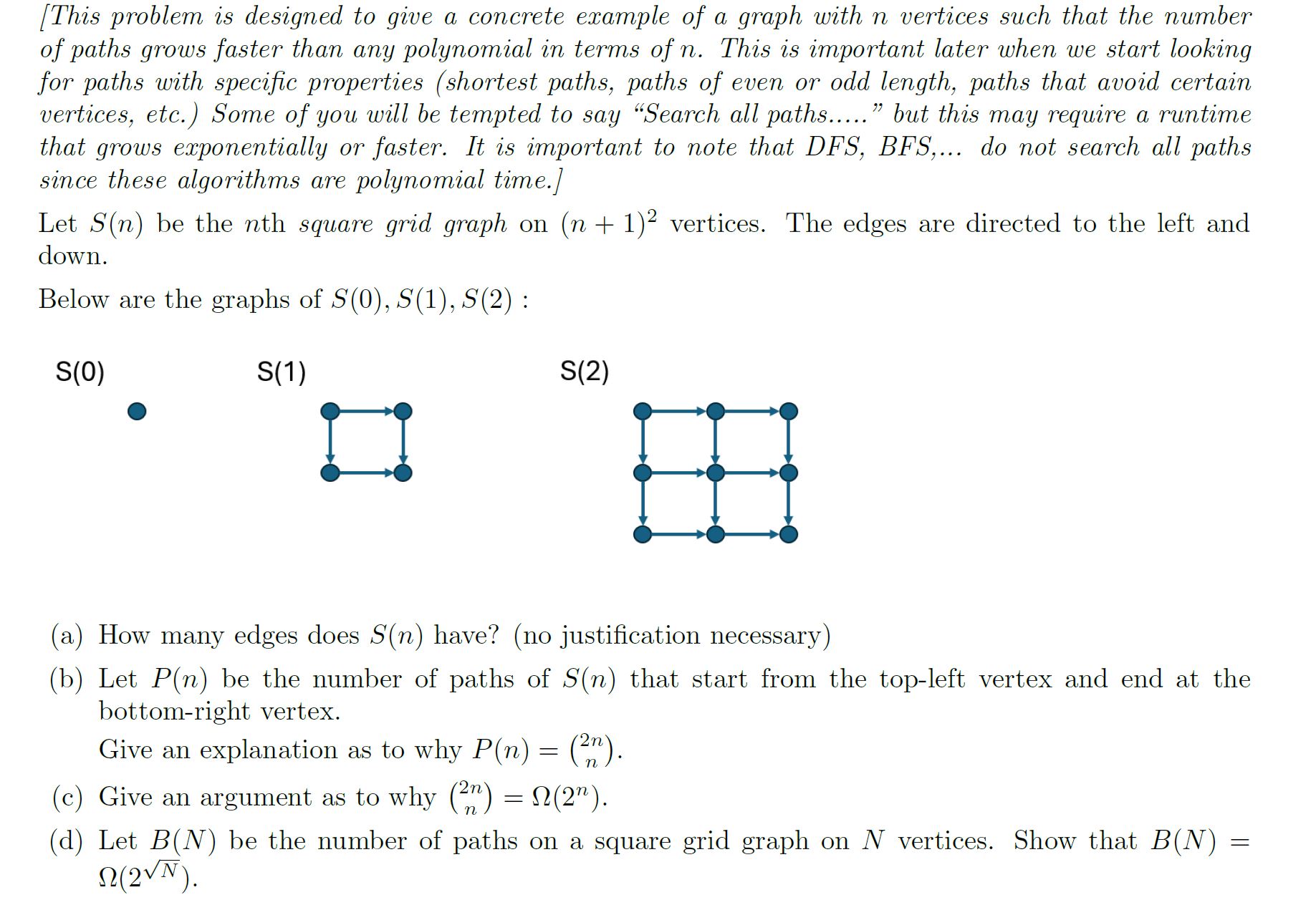
Let $S(n)$ be the $n$th square grid graph on $(n+1{)}^2$ vertices. The edges are directed to the left and

down.

Below are the graphs of $S(0),S(1),S(2)$ :

$S(0)$

$S(1)$

$($a$)$ How many edges does $S(n)$ have? $($no justification necessary$)$

$($b$)$ Let $P(n)$ be the number of paths of $S(n)$ that start from the top$-$left vertex and end at the

bottom$-$right vertex.

Give an explanation as to why $P(n)=(\frac{2n}{n}).$

$($c$)$ Give an argument as to why $(\frac{2n}{n})=(2^n).$

$($d$)$ Let $B(N)$ be the number of paths on a square grid graph on $N$ vertices. Show that $B(N)=$

$(2^{\sqrt[\phantom{2}]{N}}).$