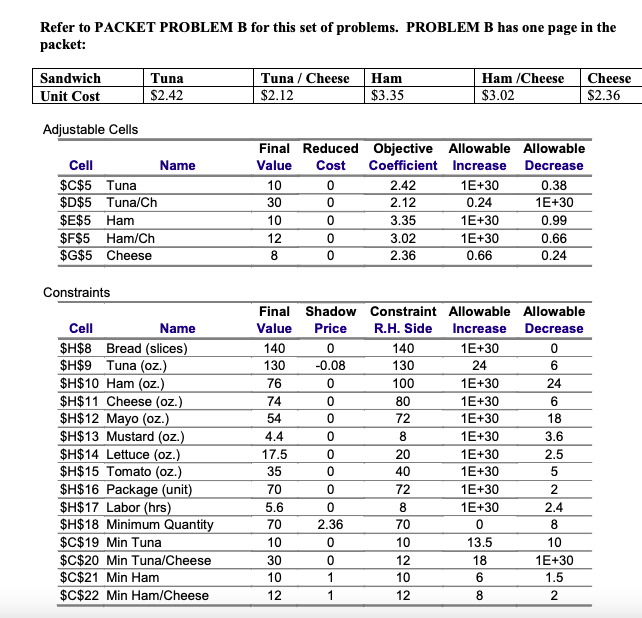
Question: This production plan is a linear program to determine the most economical mix of subs for a catering firm to provide for a wedding. The
This production plan is a linear program to determine the most economical mix of subs for a catering firm to provide for a wedding. The wedding planner has asked the catering firm to provide 70 subs in a variety to include tuna, tuna and cheese, ham, ham and cheese and cheese. They have specified a minimum of 10 each of tuna and ham, and 12 each of tuna/cheese and ham/cheese.
The catering company uses the following resources: bread, tuna, ham, cheese, mayonnaise, mustard, lettuce, tomato, packaging material and labor hours. The companies objective is to minimize total cost for producing sandwiches.
What is the range over which the cost for cheese sandwiches could vary without changing the production plan? (Highest and lowest cost)
What is the range over which the quantity of tuna could vary without changing the combination of binding constraints? (Most and least tuna)
What would be the change in the total cost if the unit cost for tuna sandwiches increased by $0.45?
What would be the change in the total cost if the wedding planner did not want any more than 14 ham sandwiches?
If possible please show work
Refer to PACKET PROBLEM B for this set of problems. PROBLEM B has one page in the packet: Sandwich Unit Cost Tuna $2.42 Tuna / Cheese Ham $2.12 $3.35 Ham /Cheese $3.02 Cheese $2.36 Adjustable Cells Cell Name $C$5 Tuna $D$5 Tuna/Ch $E$5 Ham $F$5 Ham/ch $G$5 Cheese Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase Decrease 10 0 2.42 1E+30 0.38 30 0 2.12 0.24 1E+30 10 0 3.35 1E+30 0.99 12 0 3.02 1E+30 0.66 8 0 2.36 0.66 0.24 Constraints Cell Name $H$8 Bread (slices) $H$9 Tuna (oz.) $H$10 Ham (oz.) $H$11 Cheese (oz.) $H$12 Mayo (oz.) $H$13 Mustard (oz.) $H$14 Lettuce (oz.) $H$15 Tomato (oz.) $H$16 Package (unit) $H$17 Labor (hrs) $H$18 Minimum Quantity $C$19 Min Tuna $C$20 Min Tuna/Cheese $C$21 Min Ham $C$22 Min Ham/Cheese Final Shadow Constraint Allowable Allowable Value Price R.H. Side Increase Decrease 140 0 140 1E+30 0 130 -0.08 130 24 6 76 0 100 1E+30 24 74 0 80 1E+30 6 54 0 72 1E+30 18 4.4 0 8 1E+30 3.6 17.5 0 20 1E+30 2.5 35 0 40 1E+30 5 70 0 72 1E+30 2 5.6 0 8 1E+30 2.4 70 2.36 70 0 8 10 0 10 13.5 10 30 0 12 18 1E+30 10 1 10 6 1.5 12 1 12 8 2Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


