This question concerns TM, M2, whose description and state diagram appear in Example

Turing machine (TM) that decides A ={ the language consisting of all strings of Os whose length is a power of 2. Give the sequence of configurations that M2 goes when started with q1000 configuration. Show the tape contents, head position and configuration for each transition.

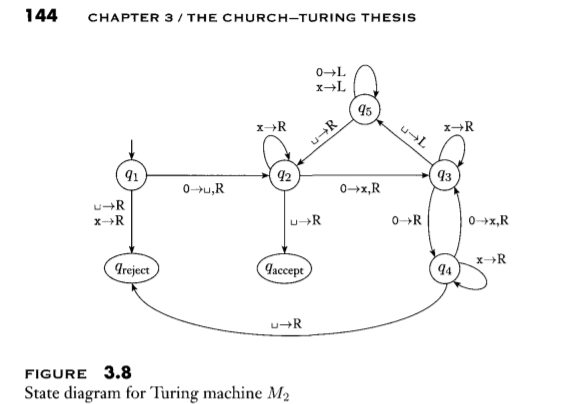
EXAMPLE 3.7 Here we describe a Turing machine (TM) M2 that decides A = {02"| n >0}, the language consisting of all strings of Os whose length is a power of 2. = M2 = "On input string w: 1. Sweep left to right across the tape, crossing off every other O. 2. If in stage 1 the tape contained a single 0, accept. 3. If in stage 1 the tape contained more than a single 0 and the number of Os was odd, reject. 4. Return the head to the left-hand end of the tape. 5. Go to stage 1." Each iteration of stage 1 cuts the number of Os in half. As the machine sweeps across the tape in stage 1, it keeps track of whether the number of os seen is even or odd. If that number is odd and greater than 1, the original number of Os in the input could not have been a power of 2. Therefore the machine rejects in this instance. However, if the number of Os seen is 1, the original number must have been a power of 2. So in this case the machine accepts. Now we give the formal description of M2 = (0,2,1,0, 91, qaccept, Greject): Q = {91,92, 93, 94, 95, Gaccept, Greject}, . S = {0}, and r = {0,x,w}. We describe 8 with a state diagram (see Figure 3.8). The start, accept, and reject states are 41, Jaccept, and greject 144 CHAPTER 3 / THE CHURCH-TURING THESIS 0-1 XL 95 X-R u-L *R -+R 91 92 93 0- ,R 0+,R +R X-R -R 0 R 0 XR xR Preject (9accept 94 +R FIGURE 3.8 State diagram for Turing machine M