This question considers a system with two processing units. There are two types of requests that can arrive at this system:

$$ The Type $1$ requests require only one processing unit. These requests arrive according

to a Poisson distribution with a mean rate of $\backslash$lambda $1.$ These requests require a processing

time which is exponentially distributed with a mean processing time of $1$

$1$

$.$

$$ Each Type $2$ request requires two processing units simultaneously. By $$simultaneously$,$ we mean that a Type $2$ request can only be admitted into the two processing

units when both processing units are available. If admitted, both processing units will

start to work on the admitted request at the same time and they will complete the

request at the same time.

Type $2$ requests arrive at the system according to a Poisson distribution with a mean

rate of $\backslash$lambda $2.$ The above description says that a Type $2$ request requires the same amount

of processing time at each processing unit. The processing time required by a Type

$2$ request at each processing unit is exponentially distributed with a mean processing

time of $1$

$2$

$.$

The four inter$-$arrival and service time distributions are assumed to be independent.

The system has two queueing slots. One slot is reserved for Type $1$ requests only and it

has a capacity to hold exactly one Type $1$ request. The other slot can only be used to hold

Type $2$ requests and it has a capacity to hold exactly one Type $2$ request.

The rules here are:

$$ If the Type $1$ queueing slot is empty and there is a request at the Type $2$ queueing slot,

then the Type $2$ request is admitted to the processing units if both units are available;

otherwise, the request remains in the Type $2$ queueing slot.

$$ If there is a request in the Type $1$ queueing slot, then this request will be admitted into

a newly available processing unit.

Note that the second rule above covers the case when both Type $1$ and Type $2$ queueing

slots have a request each. In that case, the request in Type $1$ queueing slot will be admitted

because the second rule above gives the priority to the Type $1$ request. Note also that the

Type $2$ request in the queue will not be admitted because there will not be two processing

units available; the Type $2$ request will remain in the queue.

Note that the above rules imply that:

$$ If there is a Type $1$ request is in the queue, then it is not possible to have any idle

processing unit.

$$ If there is a Type $2$ request in the queue, then it is not possible to have two idle

processing units.$$ It is possible to have an empty Type $1$ queue, an occupied Type $2$ queue and one idle

processing unit.

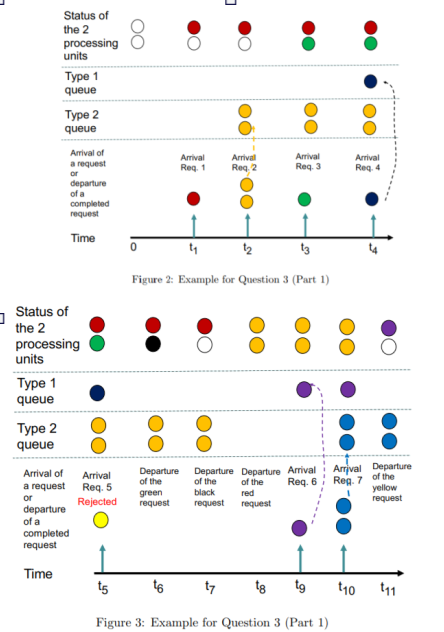
We now describe what happens when a Type $1$ request arrives. These are the possible

scenarios:

$$ If the Type $1$ queueing slot is occupied, then this request is rejected.

$$ If the Type $1$ queueing slot is not occupied, then:

$$ If at least one processing unit is idle, then this request will be admitted to an idle

processing unit and its processing will begin.

$$ If both processing units are occupied, then this request will be admitted into the

Type $1$ queueing slot.

Finally, we describe what happens when a Type $2$ request arrives. These are the possible

scenarios:

$$ If the Type $2$ queueing slot is occupied, then this request is rejected.

$$ If the Type $2$ queueing slot is not occupied, then:

$$ If both processing units are idle, then this request will be admitted to both processing units and its processing will begin.

$$ If at least one processing unit is occupied, then this request will be admitted into

the Type $2$ queueing slot.

We will now use an example to illustrate the operation of the system.

Answer the following questions:

$($a$)$ Formulate a continuous$-$time Markov chain for the system using the following $4-$tuple

as the state:

$($number of Type $1$ requests in the processing units,

number of Type $2$ requests in the processing units,

number of requests in the Type $1$ queueing slot,

number of requests in the Type $2$ queueing slot$).$

Your formulation should include a list of all possible states and the transition rates

between states. The transition rates should be expressed in terms $\backslash$lambda $1,\backslash$lambda $2,1$ and $2.($b$)$ Assuming that $\backslash$lambda $1=0\mathrm{.}9,\backslash$lambda $2=0\mathrm{.}2,1=2\mathrm{.}4$ and $2=0\mathrm{.}8.$ All these four parameters

have the unit of number of queries per some given unit time.

$($i$)$ Determine the steady state probabilities of the state of the continuous$-$time Markov

chain that you have specified in Part $($a$).$

$($ii$)$ Determine the probability that an arriving Type $2$ request will be rejected.

$($iii$)$ Determine the mean waiting time of Type $2$ requests.