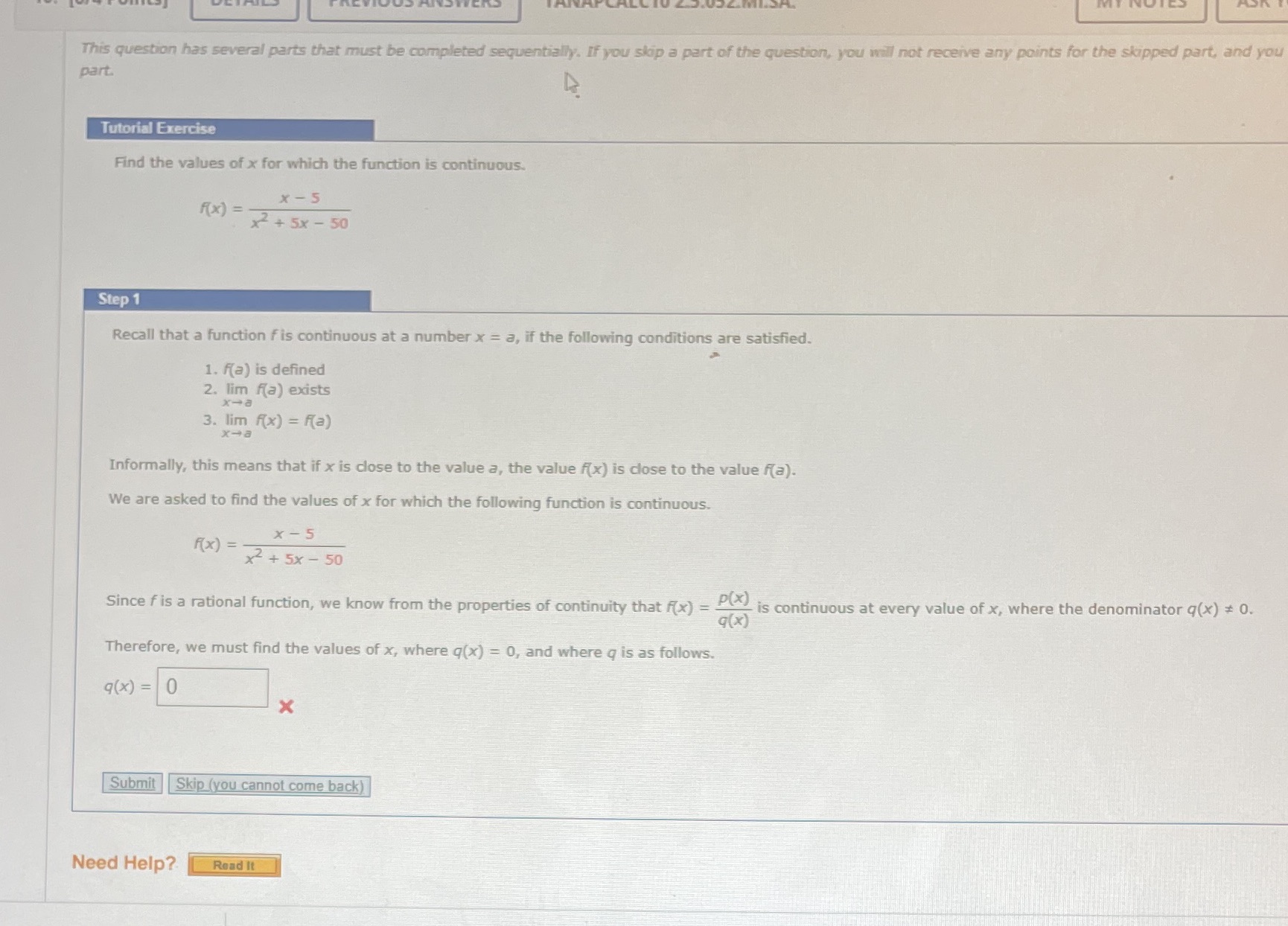
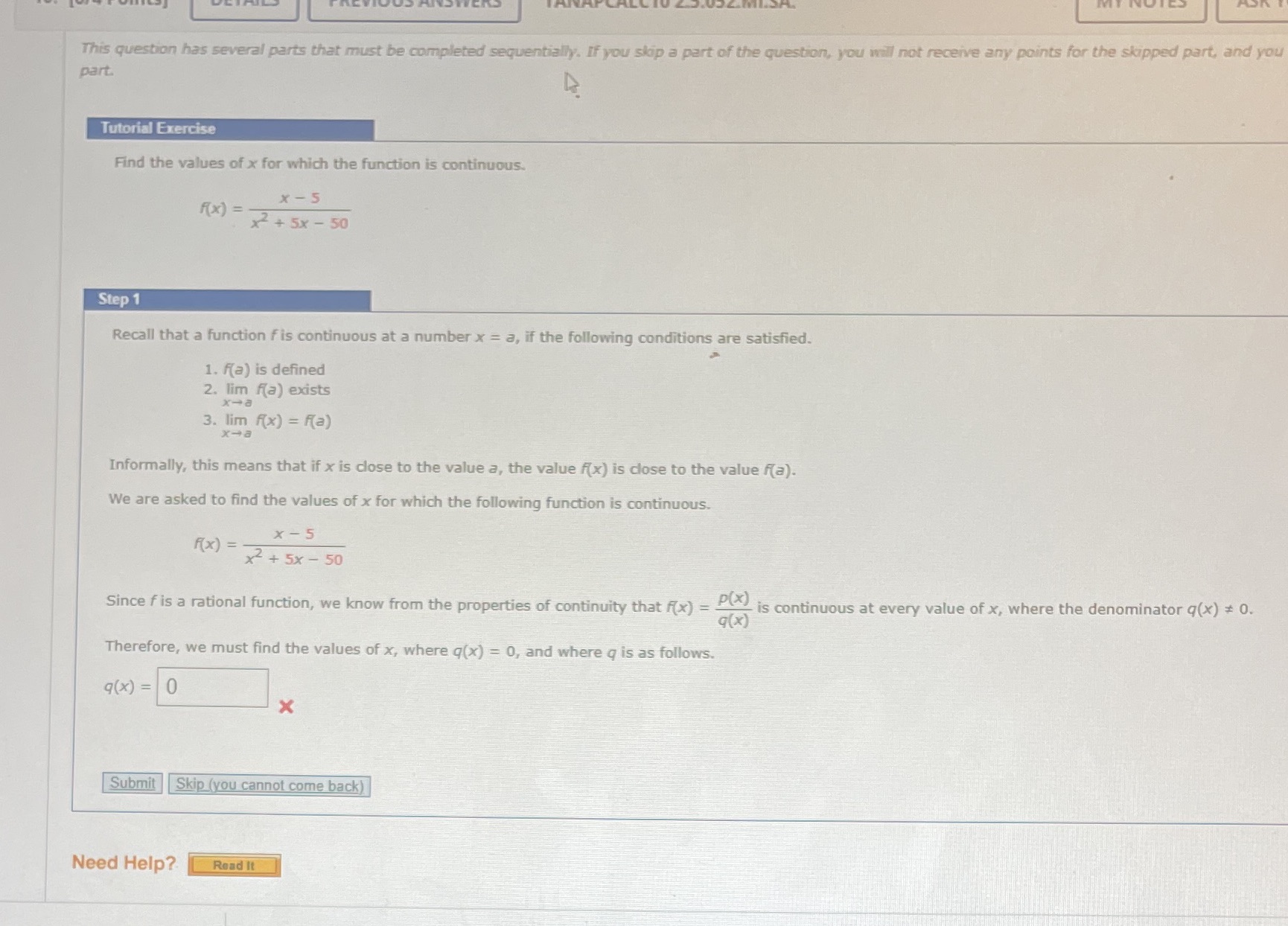
This question has several parts that must be completed sequentially. If you skip a part of the question, you will not receive any points for the skipped part, and you part. Tutorial Exercise Find the values of x for which the function is continuous. x - 5 RX ) = - x2 + 5x - 50 Step 1 Recall that a function fis continuous at a number x = a, if the following conditions are satisfied. 1. Ra) is defined 2. lim f(a) exists x -a 3. lim ((x) = R(a) x-a Informally, this means that if x is close to the value a, the value (x) is close to the value R(a). We are asked to find the values of x for which the following function is continuous. x - 5 R(x ) = x2+ 5x - 50 Since f is a rational function, we know from the properties of continuity that f(x) = is continuous at every value of x, where the denominator q(x) * 0. q(x) Therefore, we must find the values of x, where q(x) = 0, and where q is as follows. 9(x) = 0 X Submit Skip (you cannot come back) Need Help? Read It