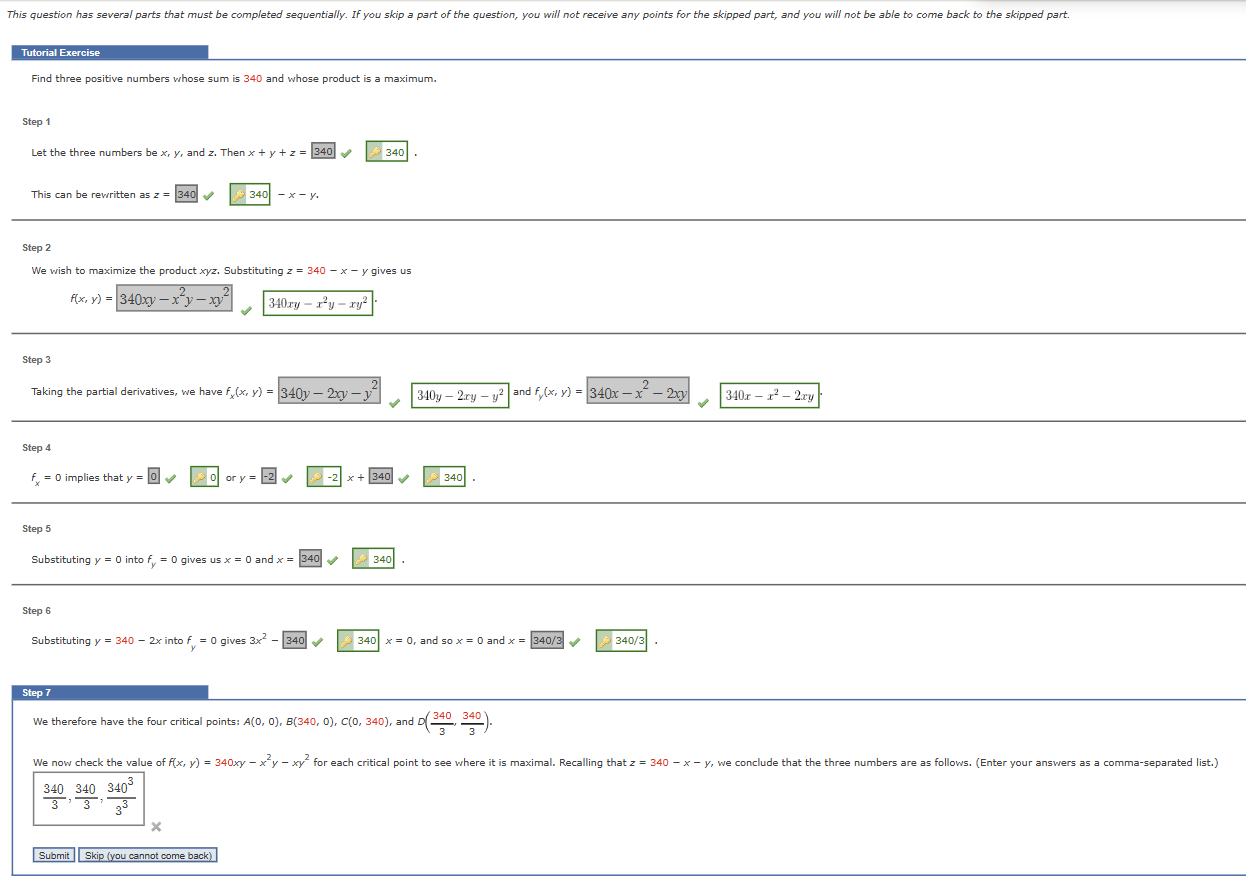
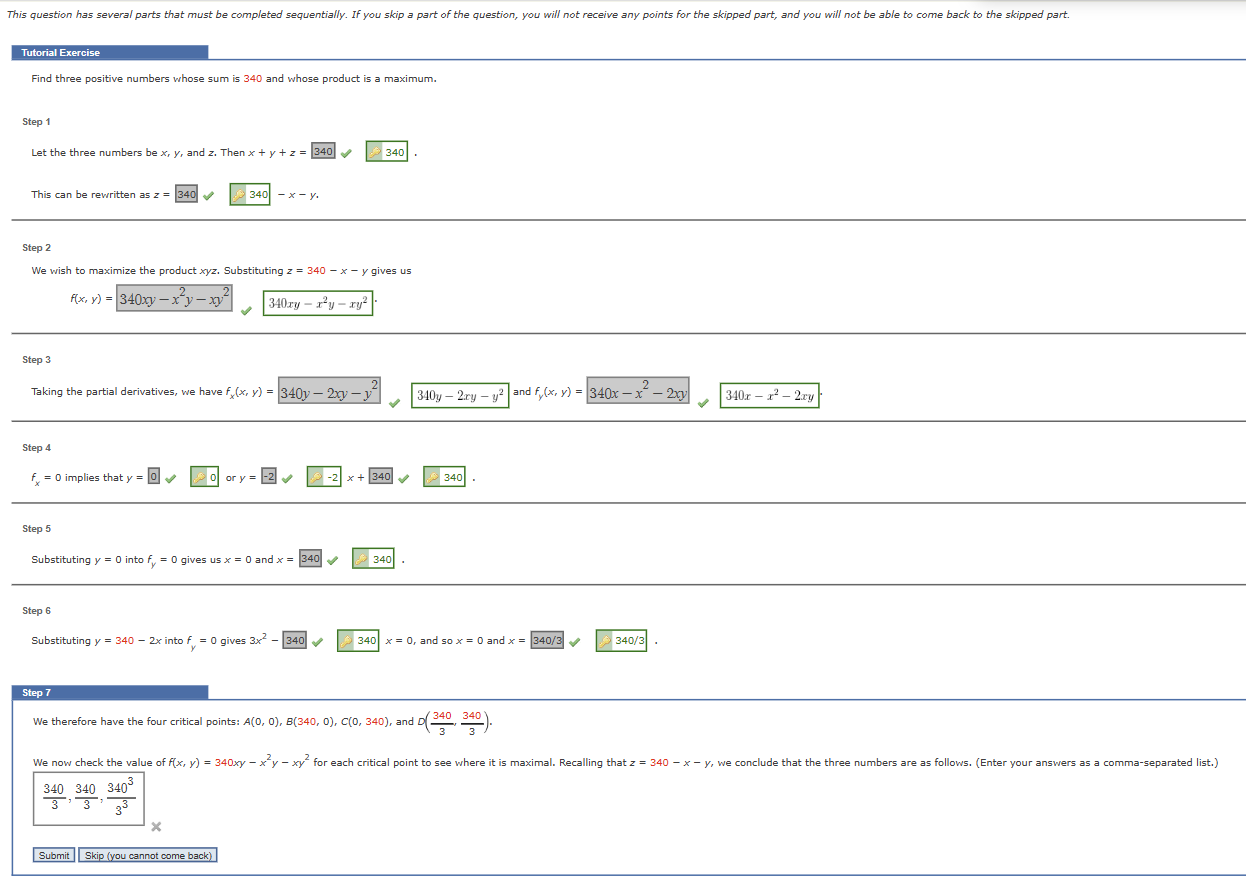
This question has several parts that must be completed sequentially. If you skip a part of the question, you will not receive any points for the skipped part, and you will not be able to come back to the skipped part. Tutorial Exercise Find three positive numbers whose sum is 340 and whose product is a maximum. Step 1 Let the three numbers be x, y, and z. Then x + y + z = 340 340 This can be rewritten as z = 340 340 - X - y. Step 2 We wish to maximize the product xyz. Substituting z = 340 - x - y gives us Ax, y) = 340xy - x y - xy 340xy - a-y - xy? Step 3 Taking the partial derivatives, we have f,(x, y) = 340y - 2xy - > 340y - 2ry - yz and f,(x, y) = 340x - x - 2xy 340.x - x2 - 2ry Step 4 f = 0 implies that y = 0 | 0 ory = -2 - -2 x+ 340 4 340. Step 5 Substituting y = 0 into f = 0 gives us x = 0 and x = 340 340 Step 6 Substituting y = 340 - 2x into f = 0 gives 3x2 - 340 4 340 x = 0, and so x = 0 and x = 340/3 340/3 Step 7 We therefore have the four critical points: A(0, 0), B(340, 0), C(0, 340), and D( 340, 340 ). We now check the value of f(x, y) = 340xy - x y - xy for each critical point to see where it is maximal. Recalling that z = 340 - x - y, we conclude that the three numbers are as follows. (Enter your answers as a comma-separated list.) 340 340 340 3 33 Submit Skip (you cannot come back)