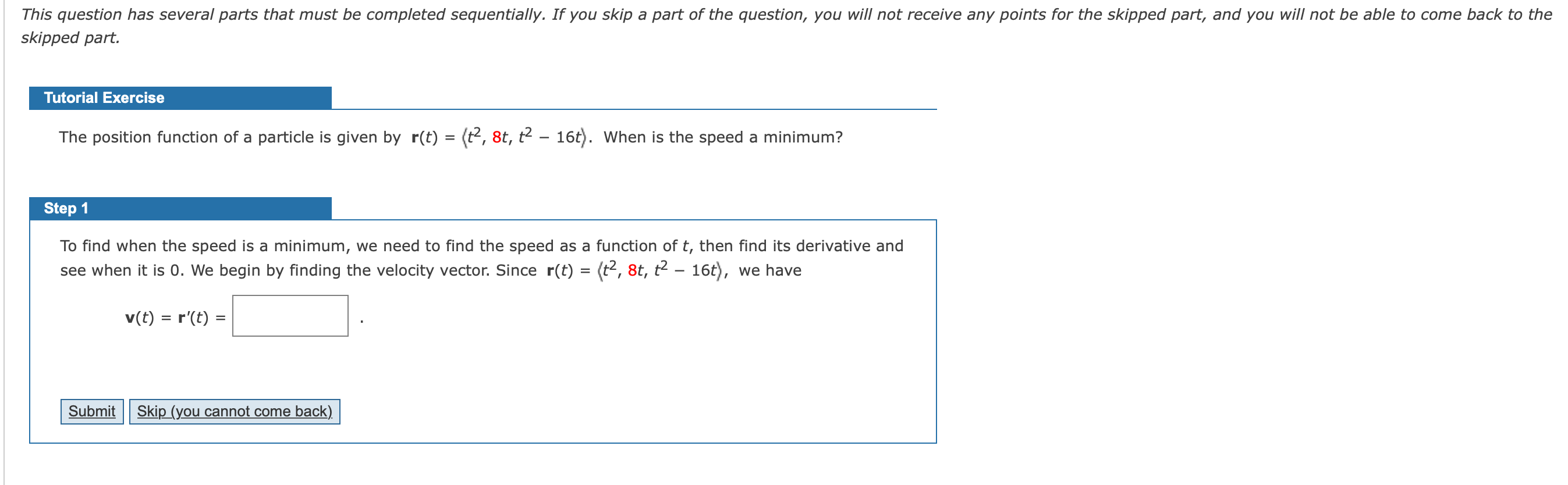
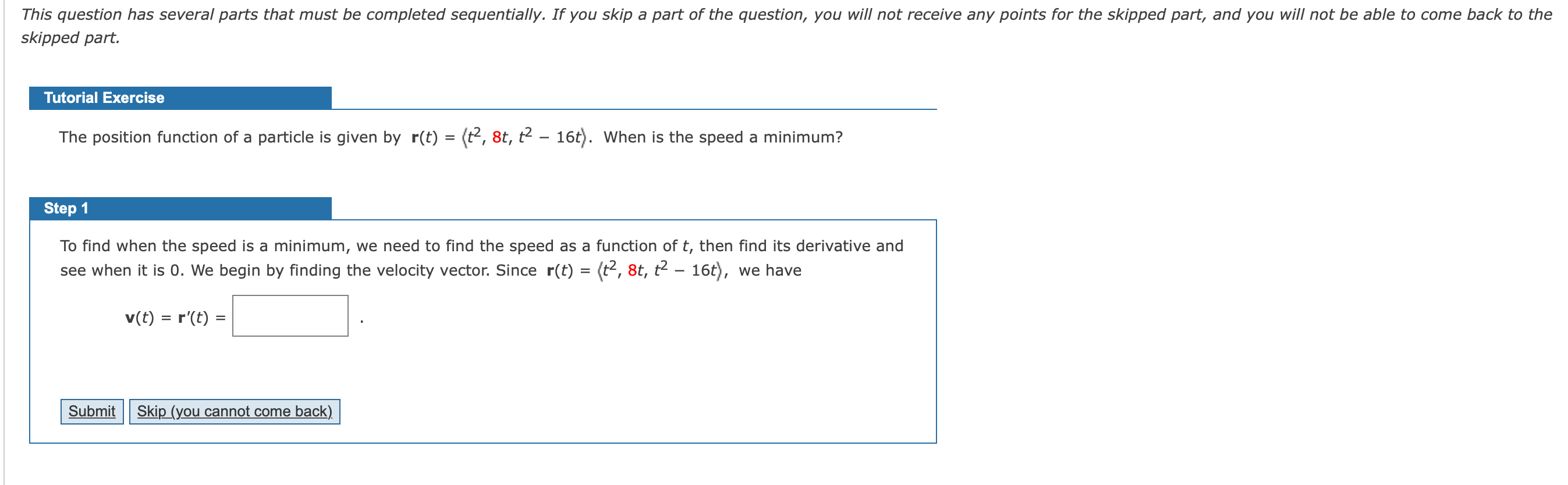
This question has several parts that must be completed sequentially. If you skip a part of the question, you will not receive any points for the skipped part, and you will not be able to come back to the skipped part. Tutorial Exercise The position function of a particle is given by r(t) = (t2, 8t, t2 - 16t). When is the speed a minimum? Step 1 To find when the speed is a minimum, we need to find the speed as a function of t, then find its derivative and see when it is 0. We begin by finding the velocity vector. Since r(t) = (t2, 8t, t2 - 16t), we have v(t) = r'(t) = Submit Skip (you cannot come back)