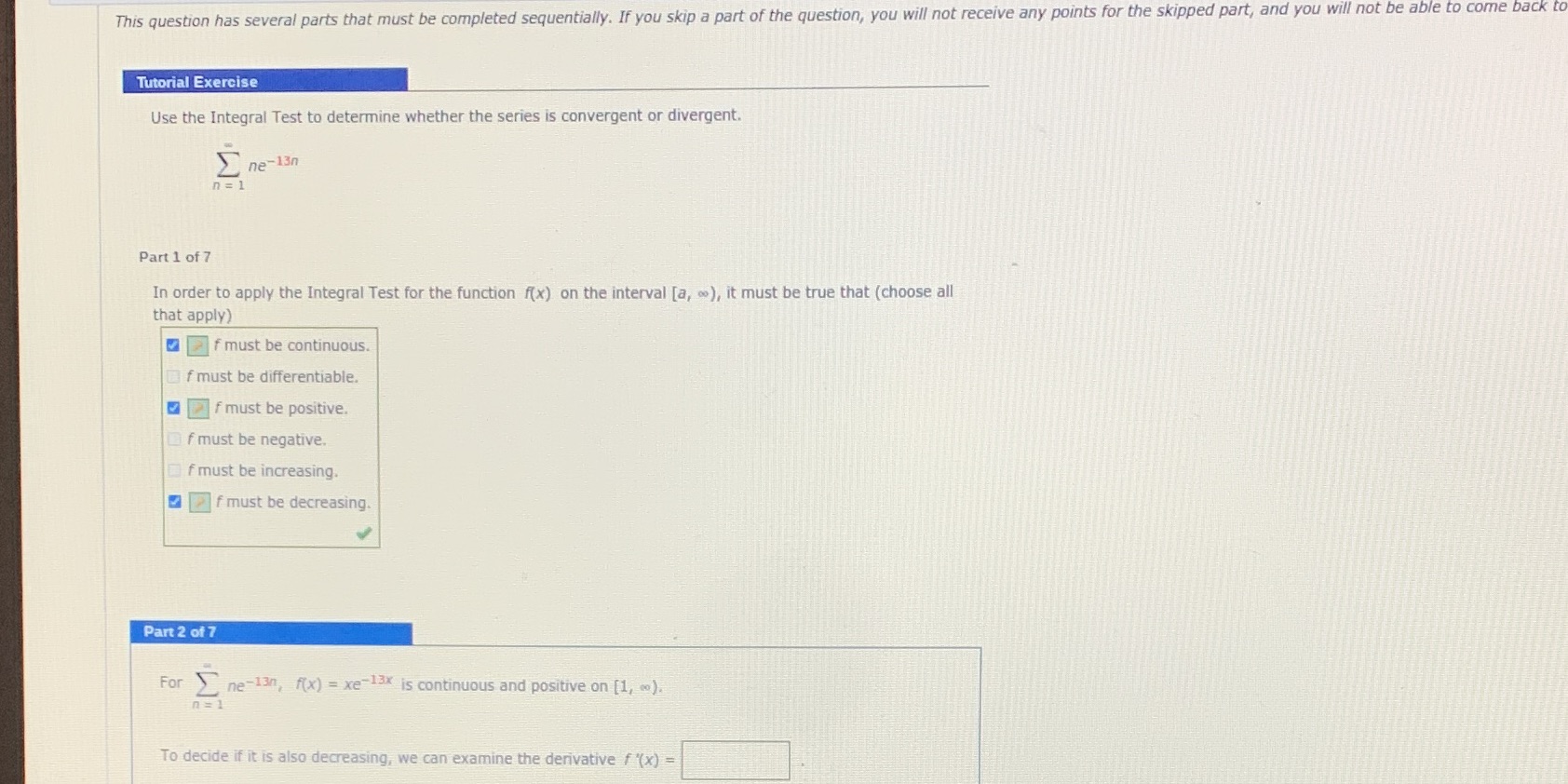
This question has several parts that must be completed sequentially. If you skip a part of the question, you will not receive any points for the skipped part, and you will not be able to come back to Tutorial Exercise Use the Integral Test to determine whether the series is convergent or divergent. _ne - 13n n = 1 Part 1 of 7 In order to apply the Integral Test for the function f(x) on the interval [a, .), it must be true that (choose all that apply) f must be continuous. Of must be differentiable. |f must be positive. Of must be negative. f must be increasing. |f must be decreasing. Part 2 of 7 For > ne-130, f(x) = xe-13x is continuous and positive on [1, ). 1 = 1 To decide if it is also decreasing, we can examine the derivative f '(x) =