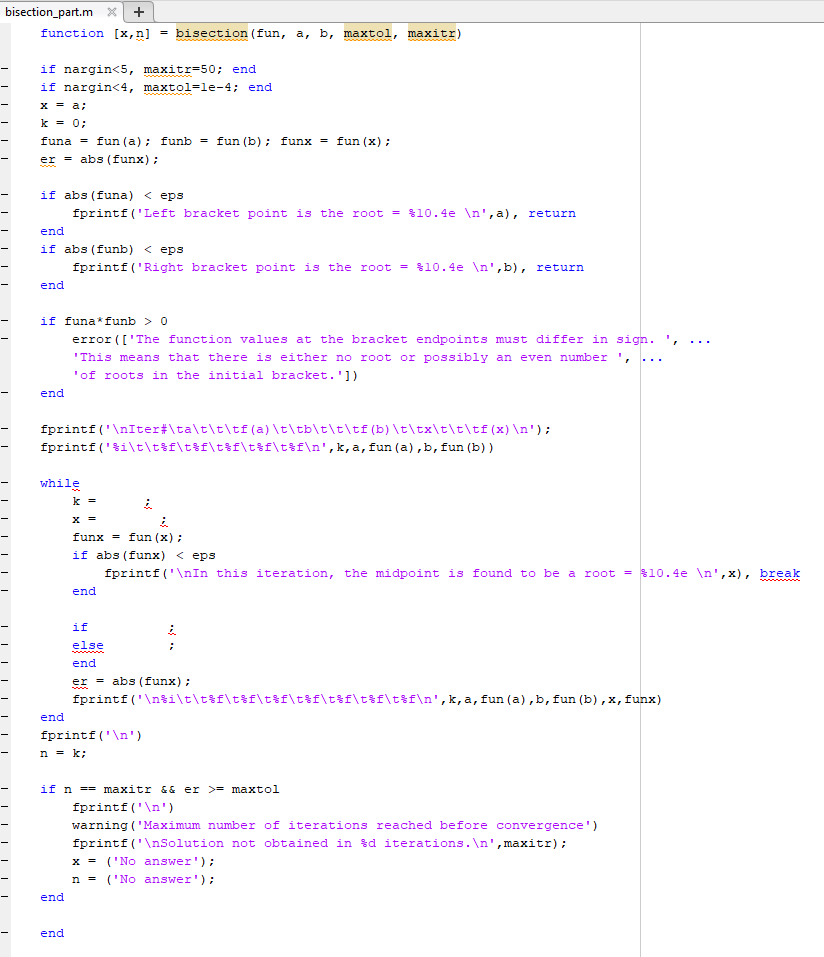
This question helps students to understand how to develop a numerical solver to find the roots of an algebraic equation. a) Write a MATLAB user-defined function that solves for a root of an equation f(x) = 0 using the bisection method. Name the function f(1) = 1 + cosh(1) cos(1) = 0 The input argument fun is a name for the function f(x) (it is a dummy name for the function that is imported into bisection), a and b are two points that bracket the root, maxtol is the maximum tolerance and maxitr is the maximum number of iterations. The program will stop if either of the following conditions is met: The approximate error (abs(fun(x)) is less than the maximum tolerance (maxtol). The number of iterations exceeds the maximum number of iterations (maxitr) Output the following values at each iteration (k) using fprintf to allow checking of results within the loop k, a, f(a), b, f(b), x, f(x) A partially completed code is provided for your reference. Complete the code by following the logic and codes for the bisection method developed in the lecture notes. b) Apply your bisection code to find all the roots of the following polynomial and compare your results to those obtained in Problem 1. f(x) = 2x3 7x2 5x + 3 bisection_part.mx + function [x, n] = bisection (fun, a, b, maxtol, maxitr) if nargin 0 error(['The function values at the bracket endpoints must differ in sign. ', 'This means that there is either no root or possibly an even number', 'of roots in the initial bracket.']) end fprintf(" Iter#\ta\t\t\tf(a)\t\tb\t\t\tf(b)\t\tx\t\t\tf(x) '); fprintf('i\t\tsf\t%f\t%f\t%[\t%f ',k, a, fun(a),b, fun (b)) while funx = fun (x); if abs (funx) = maxtol fprintf(' ') warning ("Maximum number of iterations reached before convergence') fprintf(" Solution not obtained in $d iterations. ',maxitr); ('No answer'); n = ('No answer'); end end This question helps students to understand how to develop a numerical solver to find the roots of an algebraic equation. a) Write a MATLAB user-defined function that solves for a root of an equation f(x) = 0 using the bisection method. Name the function f(1) = 1 + cosh(1) cos(1) = 0 The input argument fun is a name for the function f(x) (it is a dummy name for the function that is imported into bisection), a and b are two points that bracket the root, maxtol is the maximum tolerance and maxitr is the maximum number of iterations. The program will stop if either of the following conditions is met: The approximate error (abs(fun(x)) is less than the maximum tolerance (maxtol). The number of iterations exceeds the maximum number of iterations (maxitr) Output the following values at each iteration (k) using fprintf to allow checking of results within the loop k, a, f(a), b, f(b), x, f(x) A partially completed code is provided for your reference. Complete the code by following the logic and codes for the bisection method developed in the lecture notes. b) Apply your bisection code to find all the roots of the following polynomial and compare your results to those obtained in Problem 1. f(x) = 2x3 7x2 5x + 3 bisection_part.mx + function [x, n] = bisection (fun, a, b, maxtol, maxitr) if nargin 0 error(['The function values at the bracket endpoints must differ in sign. ', 'This means that there is either no root or possibly an even number', 'of roots in the initial bracket.']) end fprintf(" Iter#\ta\t\t\tf(a)\t\tb\t\t\tf(b)\t\tx\t\t\tf(x) '); fprintf('i\t\tsf\t%f\t%f\t%[\t%f ',k, a, fun(a),b, fun (b)) while funx = fun (x); if abs (funx) = maxtol fprintf(' ') warning ("Maximum number of iterations reached before convergence') fprintf(" Solution not obtained in $d iterations. ',maxitr); ('No answer'); n = ('No answer'); end end