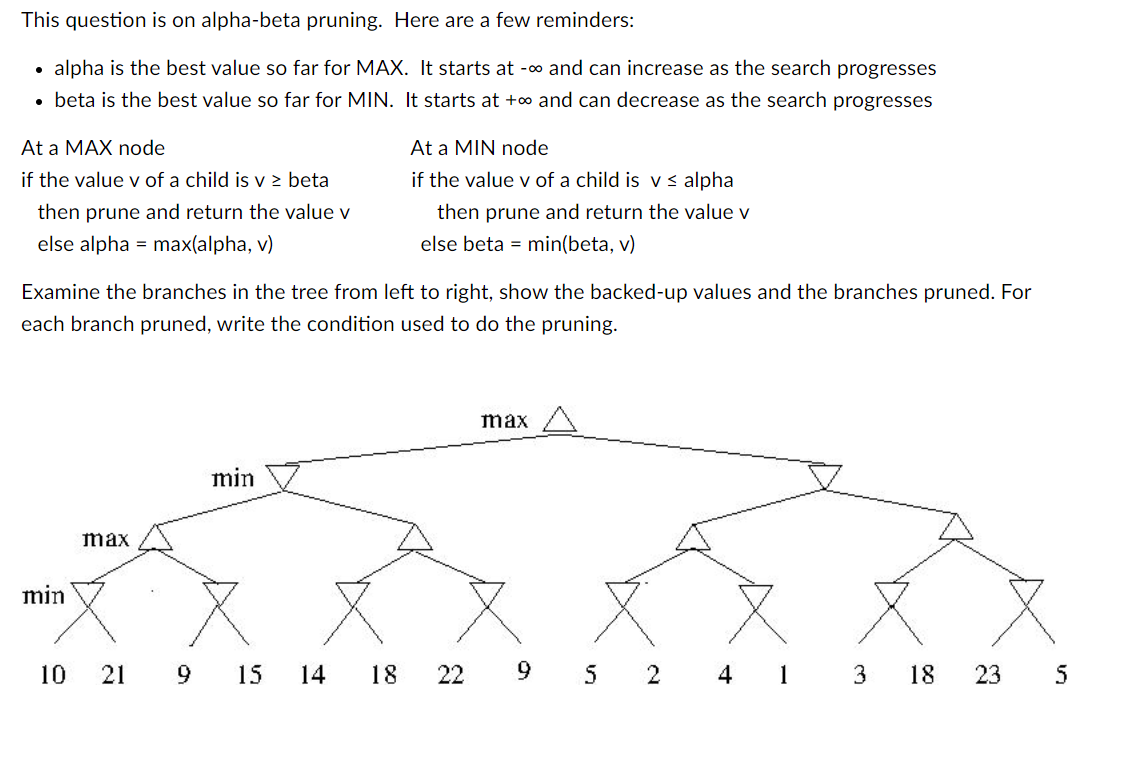
Question: This question is on alpha - beta pruning. Here are a few reminders: alpha is the best value so far for MAX. It starts at
This question is on alphabeta pruning. Here are a few reminders:
alpha is the best value so far for MAX. It starts at oo and can increase as the search progresses
beta is the best value so far for MIN. It starts at oo and can decrease as the search progresses
At a MAX node
if the value v of a child is v beta
then prune and return the value v
else alpha max alpha, v
At a MIN node
if the value v of a child is v alpha
then prune and return the value v
else beta min beta, v
Examine the branches in the tree from left to right, show the backedup values and the branches pruned. For
each branch pruned, write the condition used to do the pruning.
A drawback of A is its memory requirement since the frontier might get very large. Suppose you modify A as follows: You obtain by some method a path to a goal node and its associated cost fGoalC This cost is not necessarily minimal but it gives an upper bound on the minimal cost. Now use A with an admissible h function and discard immediately any frontier nodes reached whose f values are greater than C Answer these questions, explaining your reasoning.
Is this modified A algorithm guaranteed to find an optimal solution if one exists or not?
Since the algorithm might discard nodes in the frontier, does it mean that fewer nodes are expanded?
Does this modification reduce the total storage requirements?
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


