This question is super hard. Can any tutor see the following attachment to help me out?

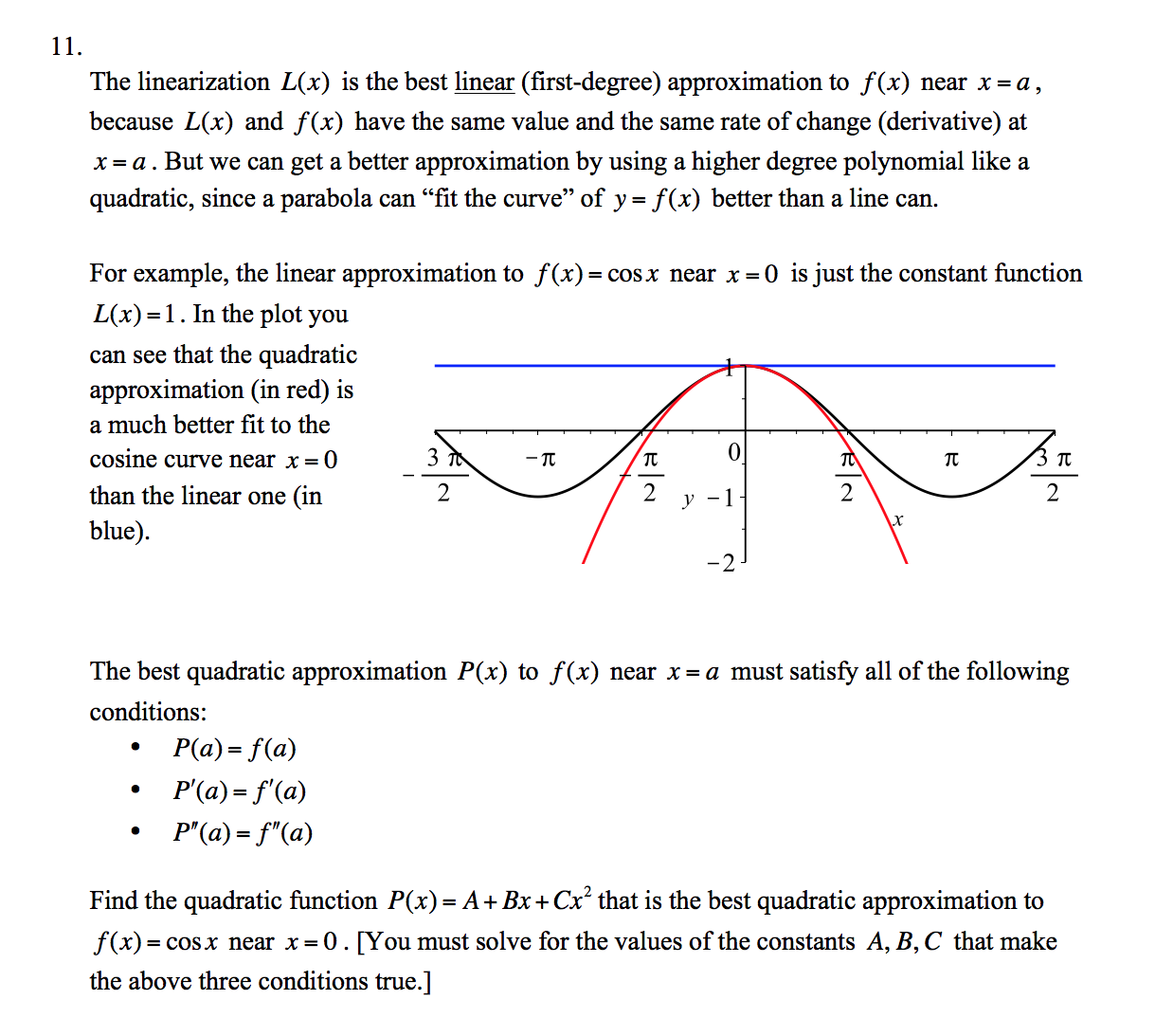
11. The linearization L(x) is the best linear (rst-degree) approximation to f (x) near x = a , because L(x) and f (x) have the same value and the same rate of change (derivative) at x = a . But we can get a better approximation by using a higher degree polynomial like a quadratic, since a parabola can \"t the curve\" of y = f (at) better than a line can. For example, the linear approximation to f (x) = cosx near x = 0 is just the constant function L(x) = 1 . In the plot you can see that the quadratic approximation (in red) is a much better t to the cosine curve near x = 0 than the linear one (in blue). The best quadratic approximation P(x) to f (x) near x = a must satisfy all of the following conditions: ' P(a) = f (a) ' P'(a) = f '(a) ' P\"(a) = f "(61) Find the quadratic function P(x) = A + Bx + 01:2 that is the best quadratic approximation to f (x) = cosx near as = 0 . [You must solve for the values of the constants A, B, C that make the above three conditions true.]