This question refers to dataset 7.16. a. Given the Time Series Plot, ACF Plot, Partial ACF Plot of original series (Figure 1 & Figure 2), conclude whether this dataset is stationary or not? (5 marks) b. Given the ACF Plot and Partial ACF Plot of the seasonal differenced series (Figure 3 & Figure 4), suggest at least 2 candidate ARIMA(p,d,q)(P,D,Q)(12) models for this time series and briefly explain why.

c. Use Minitab to find residual mean squares (MS) of the candidate model(s), then conclude on the best fit ARIMA model. (5 marks) d. Use Minitab to find set of coefficients of the best fit ARIMA(p,d,q)(P,D,Q)(12) model, then write the estimated equation of this model. (5 marks)

e. Use the above best fit ARIMA model to find the forecast value for t=91 (Residuals can be concluded from Minitab's output). (5 marks)

Month, t	Observation, Y[t]
1	101
2	84
3	54
4	39
5	26
6	40
7	99
8	148
9	147
10	134
11	106
12	83
13	76
14	63
15	57
16	37
17	32
18	22
19	20
20	23
21	30
22	50
23	61
24	59
25	64
26	58
27	44
28	26
29	24
30	18
31	16
32	17
33	21
34	28
35	30
36	51
37	62
38	57
39	46
40	40
41	32
42	23
43	20
44	18
45	24
46	33
47	52
48	66
49	78
50	83
51	87
52	64
53	44
54	24
55	29
56	73
57	138
58	154
59	119
60	102
61	79
62	53
63	40
64	27
65	31
66	56
67	78
68	114
69	140
70	112
71	82
72	80
73	70
74	55
75	37
76	23
77	20
78	39
79	71
80	110
81	112
82	93
83	75
84	60
85	63
86	46
87	32
88	23
89	53
90	90

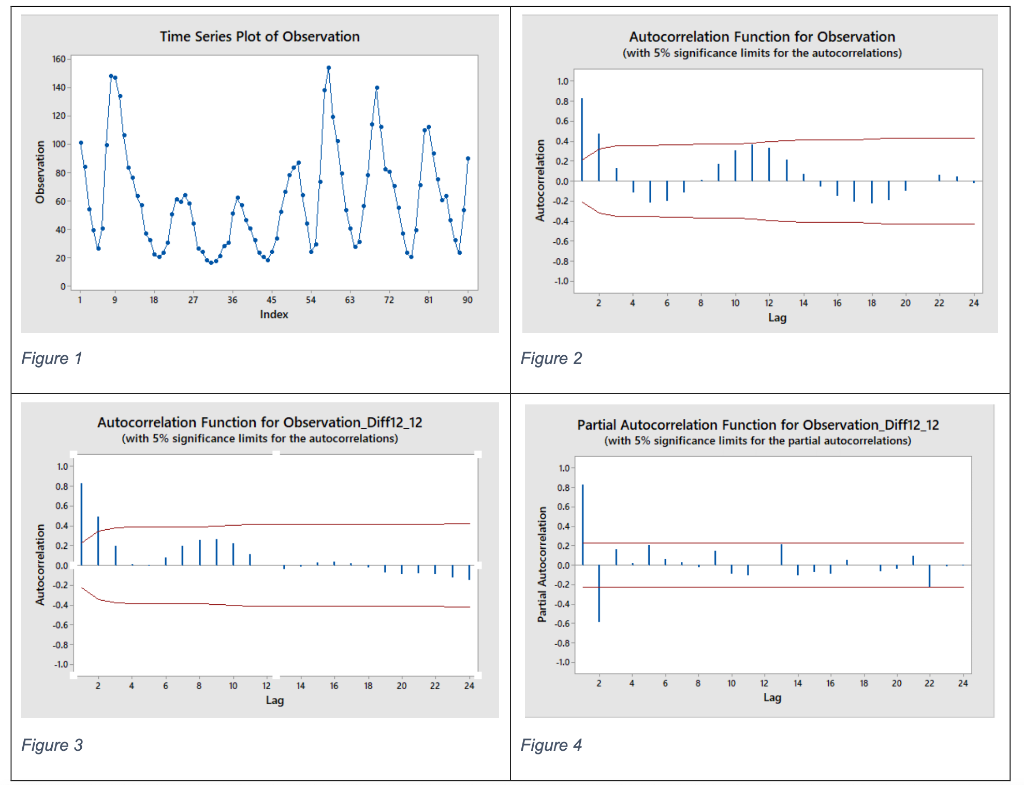
Time Series Plot of Observation Autocorrelation Function for Observation (with 5% significance limits for the autocorrelations) 160 1.0 140 0.8 120 0.6 100 0.4 0.2 Observation 80 1111 Autocorrelation 47 0.0 60 -0.2 N -0.4 40 -0.6 20 -0.8 -1.0 0 1 9 9 18 27 36 54 63 72 81 90 2 4 45 Index 6 8 10 14 16 18 20 22 24 12 Lag Figure 1 Figure 2 Autocorrelation Function for Observation_Diff12_12 (with 5% significance limits for the autocorrelations) Partial Autocorrelation Function for Observation_Diff12_12 (with 5% significance limits for the partial autocorrelations) 1.0 1.0 0.8 0.8 0.6 0.6 0.4 0.4 0.2 0.2 Autocorrelation 0.0 Partial Autocorrelation 0.0 -0.2 -0.2 -0.4 -0.4 -0.6 -0.6 -0.8 -0.8 -1.0 -1.0 2 4 6 8 10 14 16 18 20 22 4 24 2 6 8 10 14 16 18 20 22 24 12 Lag 12 Lag Figure 3 Figure 4