This question should be complete.

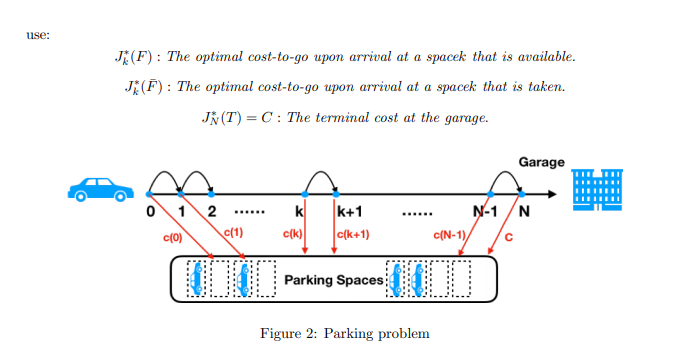
A student is looking for a parking space on the way to his/her office. There are N spaces leading up to his/her office, and a garage at the office. His/Her goal is to park as close to the close as possible. He/She starts at space 0 and traverses the parking spaces sequentially, i.e. from space k he/she goes next to space k + 1, and never go back. Each parking space k costs e(k) = N k, and is free with probability p(k) independently of whether other parking spaces are free or not. If he/she reaches the last parking space and does not park there or there is no space available, he/she must parking at the garage with costs C. The student can observe whether a parking space is free only when he reaches it. If it is free, he/she has two options, either to park or go and check the next space, if not he could do nothing but go forward. The problem is to find the minimum expected cost parking policy. We formulate the problem as a DP problem with N stages, corresponding to the parking spaces, and an terminal state T; see figure 2 At each stage k = 0, ..., N 1, we have two states (k, F) and %3D (k, F, corresponding to space k is available or not. The action is to park or continue at state (k, F) and there is no action at states (k, F) and the garage(stage N). (1) Written the Bellman Equation for stage k = 0,..., N 1. Here are some notations you may use: J(F) : The optimal cost-to-go upon arrival at a spacek that is available. JE(F) : The optimal cost-to-go upon arrival at a spacek that is taken. JN (T) = C : The terminal cost at the garage. Garage N-1 /N o\1 2 k+1 ...... c(k) c(k+1) c(1) c(0) c{N-1)/ Parking Spaces; Figure 2: Parking problem A student is looking for a parking space on the way to his/her office. There are N spaces leading up to his/her office, and a garage at the office. His/Her goal is to park as close to the close as possible. He/She starts at space 0 and traverses the parking spaces sequentially, i.e. from space k he/she goes next to space k + 1, and never go back. Each parking space k costs e(k) = N k, and is free with probability p(k) independently of whether other parking spaces are free or not. If he/she reaches the last parking space and does not park there or there is no space available, he/she must parking at the garage with costs C. The student can observe whether a parking space is free only when he reaches it. If it is free, he/she has two options, either to park or go and check the next space, if not he could do nothing but go forward. The problem is to find the minimum expected cost parking policy. We formulate the problem as a DP problem with N stages, corresponding to the parking spaces, and an terminal state T; see figure 2 At each stage k = 0, ..., N 1, we have two states (k, F) and %3D (k, F, corresponding to space k is available or not. The action is to park or continue at state (k, F) and there is no action at states (k, F) and the garage(stage N). (1) Written the Bellman Equation for stage k = 0,..., N 1. Here are some notations you may use: J(F) : The optimal cost-to-go upon arrival at a spacek that is available. JE(F) : The optimal cost-to-go upon arrival at a spacek that is taken. JN (T) = C : The terminal cost at the garage. Garage N-1 /N o\1 2 k+1 ...... c(k) c(k+1) c(1) c(0) c{N-1)/ Parking Spaces; Figure 2: Parking