This was a challenging question posed in my class. My idea is that we need to find two permutations that are not commutative. And when cubed, the result should be an identity element, which means that the cycle can only has length of 1 or 3. My instructor said that I'm on the right track, but I still struggled to find the solution. Can anyone help me with this? Thank you.

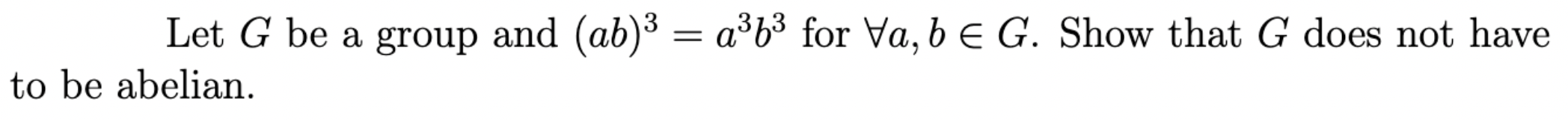
Let G be a group and (ab)3 = a363 for Va, b E G. Show that G does not have to be abelian