Fill in the blanks in python 

  

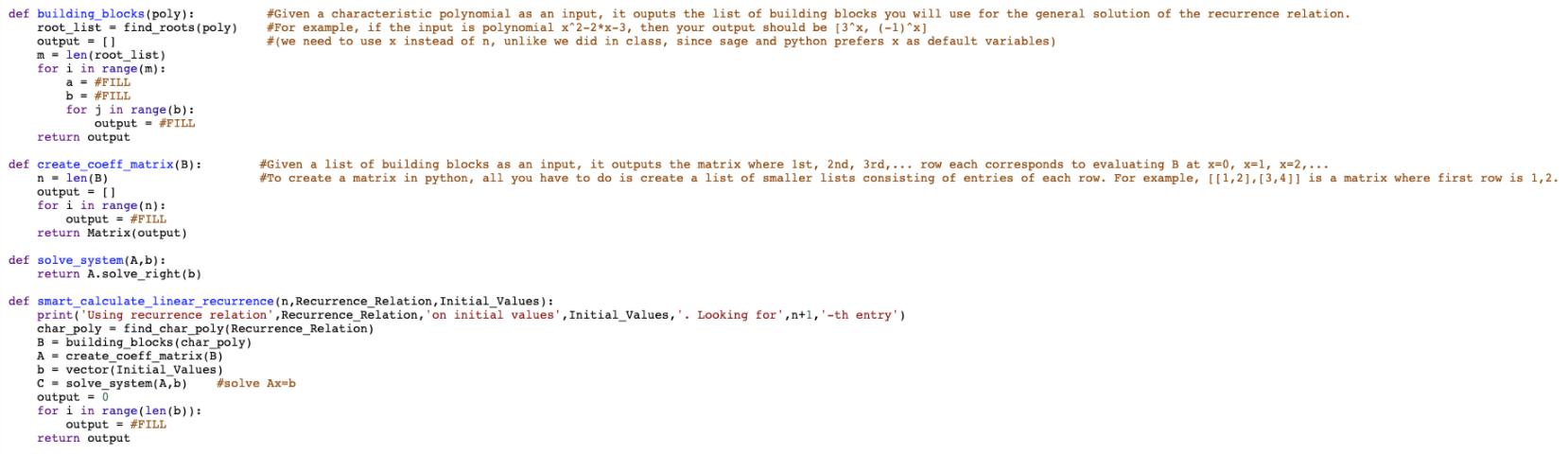
## This week we are again solving the n-th entry in a linear recurrence relation, but this time using characteristic polynomials and what we learned in class. ## Recurrence relations of a n = c_1 * a_{n-1} +c_2 a_{n-2} + ... are stored as [c_1,c_2,...] ## initial values, starting from a_0 are stored as [a_0,a_1,...] ## smart calculate linear recurrence (n, Recurrence Relation, Initial Values) calculates an given the recurrence relation and initial values. You may assume for this this function that the length of the lists are the same. ## In python (and sage), given a function f(x) of x, if you want to evaluate it at say x-3, you do f(x) (x-3). For example, (x^2-1) (x-2) will give you 3. ## If you have L, a list of functions of x, and if you want to get a list where you evaluate them at say x=3, you can do [z(x=3) for z in L] ## once you are done, ## 1. run find char poly([2,3,4,0,1]) ## 2. run building blocks (x 6 + 2*x*5 - 15*x*4 - 40*x*3 + 40*x*2 + 192*x + 144) ## 3. run create_coeff_matrix([3^x, 3^x*x, (-2) x, (-2)^x*x, (-2)^x*x^2, (-2) x*x*3]) ## 4. run smart_calculate_linear_recurrence (100,[1,1],[1,1]) ## 5. run smart_calculate_linear_recurrence (1000, [-2,15,40,-40,-192,-1441, [1,1,1,1,1,1]) def find char poly (Recurrence_Relation): 3*x^3 - 4*x^2- 1 n = len (Recurrence_Relation) poly = ##FILL for i in range (n): poly - ##FILL return poly #Given a recurrence relation, outputs the characteristic polynomial using x as a variable. For example, if the input is [2,3,4,0,1], then the output should be x*5 - 2*x^4 - def find_roots (poly): return poly.roots ()