This week we do something useful with our z-values by using them to:

• Create CONFIDENCE INTERVALS around the mean, and
• TEST HYPOTHESES to see just how "sure" we are that they are statistically supported

CONFIDENCE INTERVALS

The z-values can be used to construct a confidence interval for a PROPORTION (%)If TWO conditions about the sampling distribution and sample size are met:

1. The Sampling Distribution must be a Normal (bell) Distribution (histogram bell-shaped?), or you can Multiply the sample size times the proportion probability (np), then n times the alternate probability n (1 - p) and IF BOTH are 5 or greater, it's a Normal Distribution.
2. The Sample Size (n) must be 30 or greater.

Now let's actually calculate a Confidence Interval around a Population mean, based on SAMPLE data.

1)The 896 residents of a retirement community were tested for Covid-19 and 120 tested positive. What is the 95% confidence interval around the TRUE proportion infected? Fill in the blanks:

n = _____, sample proportion infected (p-hat) = ________; sampling proportion not infected (q-hat) = ______

? = _____ and ?/2 = ______ so, the Critical +z-value (z_c) = _________ ;

a) Calculate the Margin of Error boundary,E= z_c * SQRT [( p * q)] = ________ (don't forget this formula !)

b) Calculate the Confidence Interval: p-hat - E

c) State what this means:

2)(made-up problem)PROPORTION problem (use z)

35000 students took Stat 200 and 29000 passed. At the 1% significance level, what is the confidence interval around this proportion?

a) x = _______; n = ____________; p-hat =___________; q-hat = ___________; z_c= ____________

b) Using the formula for E, what is this margin of error?______________ (show setup and final value)

c) What is the Confidence Interval? _________

NOW,what if either or both of the two conditions required to use the critical z-values are NOT met?

We use t- values. Unlike z-values, t-values depend on sample size (n) but if "n" gets up around 1000, the t-distribution looks more and more like the z-distribution (the Normal bell curve) and the z-values and t-values are almost equal:

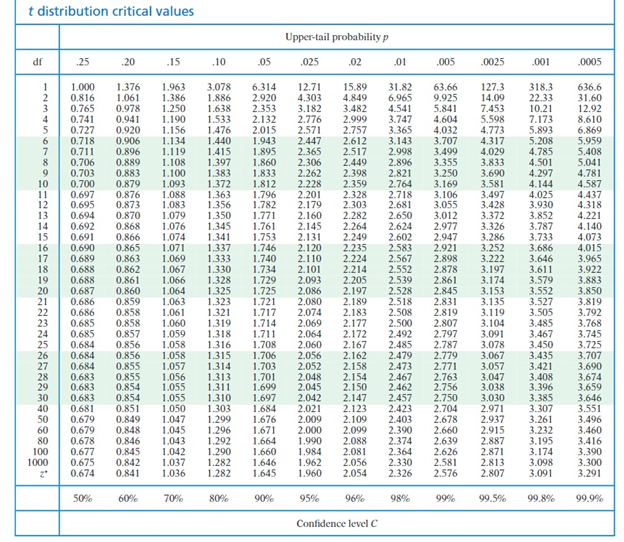
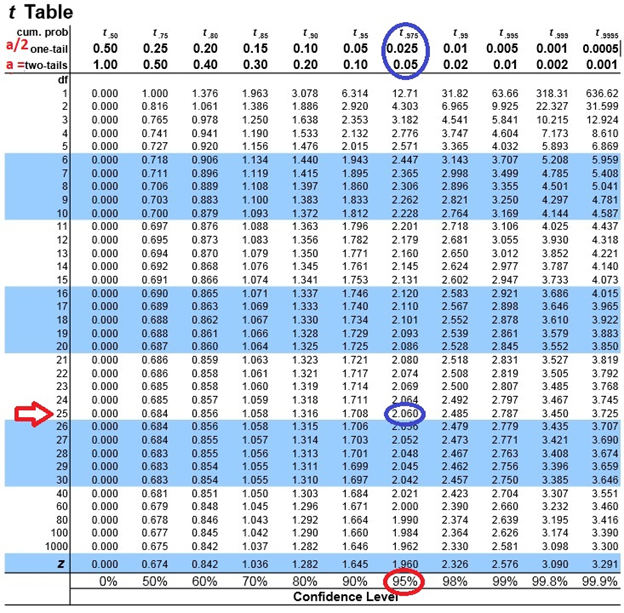
NORMAL BELL CURVE df- > 1000 9 - JP df - 3 M SD's FROM THE MEAN crit\f\f